题目内容
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
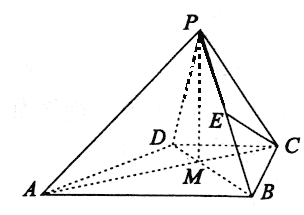
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
【答案】(Ⅰ)2;(Ⅱ)![]() .
.
【解析】
(I)延长![]() 交于点
交于点![]() ,根据线面平行的性质定理,证得
,根据线面平行的性质定理,证得![]() ,由此得到
,由此得到![]() 是
是![]() 中点,即有
中点,即有![]() .(II)在直角梯形
.(II)在直角梯形![]() 中证得
中证得![]() ,根据勾股定理证得
,根据勾股定理证得![]() ,即证得
,即证得![]() . 作
. 作![]() 交
交![]() 于
于![]() ,可得
,可得![]() 为
为![]() 的平面角,解直角三角形求得
的平面角,解直角三角形求得![]() 的余弦值.
的余弦值.
(Ⅰ)延长![]() 交于点
交于点![]() ,则
,则![]() ,故
,故![]() 是
是![]() 的中点.
的中点.
则![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,
的交线,
由![]() 平面
平面![]() ,则
,则![]()
∴![]() 为
为![]() 中点,∴
中点,∴![]() .
.
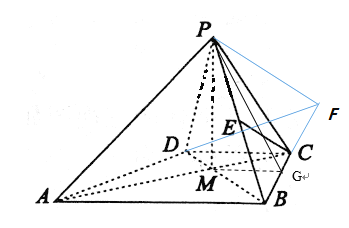
(Ⅱ)在梯形![]() 中,
中, ![]() ,
,![]() ,
,
且![]() ,
,
∴![]()
∵![]() ,∴
,∴![]() ,
,
故![]()
∴![]() ,∴
,∴![]()
且![]() ,
,
又![]() ,
,
可得![]() ,∴
,∴![]()
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .由于
.由于![]() ,则
,则![]() 平面
平面![]() ,则
,则![]() ,
,
可得![]() 为
为![]() 的平面角,且
的平面角,且![]() ,
,![]()
∴![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】已知无穷等比数列![]() 的首项、公比均为
的首项、公比均为![]() .
.
(1)试求无穷等比子数列![]() 各项的和;
各项的和;
(2)是否存在数列![]() 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为![]() ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
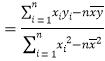 ,
,![]()
