题目内容
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)设出直线方程,结合点到直线距离公式,计算参数,即可。(2)证明得到点P为MN的中点,建立圆方程,即可。(3)将直线方程代入圆方程,结合交点个数,计算a的范围,计算直线![]() 的斜率,计算a的值,即可。
的斜率,计算a的值,即可。
(1)直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的斜率为
的斜率为![]() ,则方程为
,则方程为![]() ,即
,即![]() .又圆
.又圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,由
,由![]() ,解得
,解得![]() .
.
所以直线方程为![]() ,即
,即![]() .
.
当![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]() ,经验证
,经验证![]() 也满足条件.
也满足条件.
即直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)由于![]() ,而弦心距
,而弦心距![]() ,
,
所以![]() .
.
所以![]() 恰为
恰为![]() 的中点.
的中点.
故以![]() 为直径的圆
为直径的圆![]() 的方程为
的方程为![]() .
.
(3)把直线![]() 代入圆
代入圆![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .
.
由于直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,
故![]() ,
,
即![]() ,解得
,解得![]() .
.
则实数![]() 的取值范围是
的取值范围是![]() .
.
设符合条件的实数![]() 存在,
存在,
由于![]() 垂直平分弦
垂直平分弦![]() ,故圆心
,故圆心![]()
![]() 必在
必在![]() 上.所以
上.所以![]() 的斜率
的斜率![]() ,
,
而![]() ,
,
所以![]() .由于
.由于![]()
![]() ,
,
故不存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() .
.

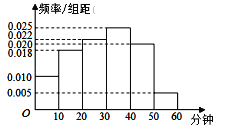
【题目】银川一中为研究学生的身体素质与课外体育锻炼时间的关系,抽取在校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() ,
,![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
课外体育不达标 | 课外体育达标 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
(2)在![]() 这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
附参考公式与:![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|