题目内容
【题目】班级新年晚会设置抽奖环节.不透明纸箱中有大小相同的红球3个，黄球2个，且这5个球外别标有数字1、2、3、4、5.有如下两种方案可供选择：
方案一：一次性抽取两球，若颜色相同，则获得奖品；
方案二：依次有放回地抽取两球，若数字之和大于5，则获得奖品.
（1）写出按方案一抽奖的试验的所有基本事件；
（2）哪种方案获得奖品的可能性更大？
【答案】（1）见解析（2）方案二获得奖品的可能性更大.
【解析】
（1）根据题意，设三个红球分别为：
，两个黄球分别为
，利用列举法一一列举出来即可；
（2）方案一二中，根据古典概型，分别求出两种方案的概率，即可得出结论.
（1）方案一中，设三个红球分别为：，两个黄球分别为，
则方案一所有可能的基本事为：
共10个基本事件.
（2）方案二中，设两次抽查取的球所标的数字分别为
、
，
则所有可能的基本事件对应的二元有序数组
表示如下表，共25个基本事件：
(1,1) | (1,2) | (1,3) | (1,4) | (1,5) |
(2,1) | (2,2) | (2,3) | (2,4) | (2,5) |
(34) | (3,2) | (3,3) | (3,4) | (3,5) |
(4,1) | (4,2) | (4,3) | (4,4) | (4,5) |
(5,1) | (5,2) | (5,3) | (5,4) | (5,5) |
方案一、方案二的基本事件总数均为有限个，
且每个基本事件发生的可能性均相同，故它们都是古典概型.
方案一，设事件
：两球颜色相同，
则包含
、
、
、
共4个基本事件，
故
.
方案二中，设事件
：两球所标数字之和大于5，
则包含
、
、
、
、
、
、
、
、
、
、
、
、
、
共15个基本事件，
故
.
因为
，所以选择方案二获得奖品的可能性更大.
阶梯计算系列答案
【题目】如图，已知抛物线
的焦点为
，椭圆
的中心在原点，
为其右焦点，点
为曲线
和
在第一象限的交点，且
．
（1）求椭圆
的标准方程；
（2）设
为抛物线
上的两个动点，且使得线段
的中点
在直线
上，
为定点，求
面积的最大值．
【题目】前段时间，某机构调查人们对屯商平台“618”活动的认可度（分为：强烈和一般两类），随机抽取了100人统计得到2×2列联表的部分数据如表：
一般 | 强烈 | 合计 | |
男 | 45 | ||
女 | 10 | ||
合计 | 75 | 100 |
（1）补全2×2列联表中的数据；
（2）判断能否有95%的把握认为人们的认可度是否为“强烈”与性别有关？
参考公式及数据：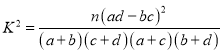
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
