题目内容
(本小题满分15分)
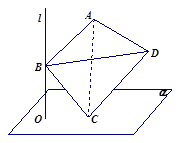
如图,已知四棱锥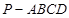 中,平面
中,平面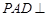 平面
平面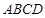 ,平面
,平面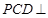 平面
平面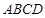 ,
,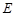 为
为
 上任意一点,
上任意一点,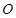 为菱形
为菱形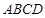 对角线的交点.
对角线的交点.
(Ⅰ)证明:平面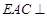 平面
平面 ;
;
(Ⅱ)若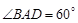 ,三棱锥
,三棱锥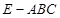 的体积是四棱锥
的体积是四棱锥
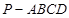 的体积的
的体积的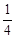 ,二面角
,二面角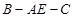 的大小为
的大小为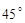 ,求
,求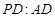

如图,已知四棱锥
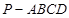 中,平面
中,平面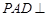 平面
平面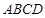 ,平面
,平面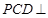 平面
平面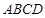 ,
,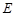 为
为 上任意一点,
上任意一点,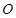 为菱形
为菱形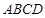 对角线的交点.
对角线的交点.(Ⅰ)证明:平面
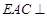 平面
平面 ;
;(Ⅱ)若
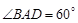 ,三棱锥
,三棱锥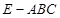 的体积是四棱锥
的体积是四棱锥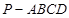 的体积的
的体积的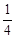 ,二面角
,二面角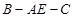 的大小为
的大小为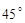 ,求
,求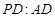

解:(Ⅰ)可证: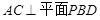 ,得平面
,得平面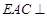 平面
平面
(Ⅱ)设三棱锥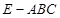 的高为
的高为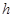 ,则
,则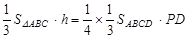
∴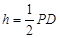 ∴
∴ ∥
∥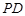
过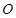 作
作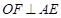 于点
于点 ,则
,则 为二面角
为二面角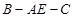 的平面角,即
的平面角,即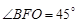
设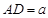 ,则
,则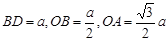 ,在
,在 中,
中,
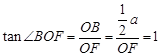 ,∴
,∴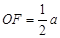 ,又在
,又在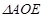 中,面积法可得
中,面积法可得
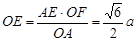 ∴
∴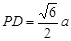
∴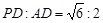
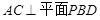 ,得平面
,得平面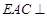 平面
平面
(Ⅱ)设三棱锥
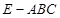 的高为
的高为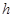 ,则
,则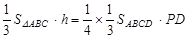
∴
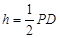 ∴
∴ ∥
∥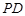
过
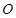 作
作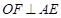 于点
于点 ,则
,则 为二面角
为二面角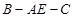 的平面角,即
的平面角,即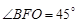
设
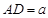 ,则
,则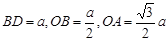 ,在
,在 中,
中,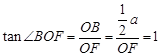 ,∴
,∴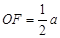 ,又在
,又在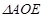 中,面积法可得
中,面积法可得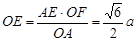 ∴
∴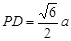
∴
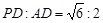
略

练习册系列答案
相关题目
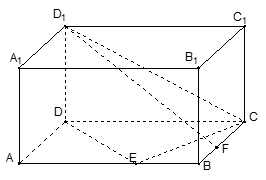
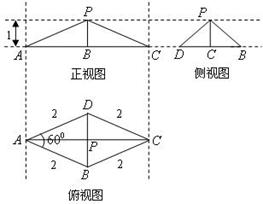
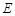 在何处时,
在何处时,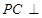 面EBD,并求出此时二面角
面EBD,并求出此时二面角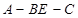 平面角的余弦值.
平面角的余弦值.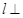 平面
平面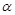 ,垂足为
,垂足为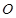 ,正四面体
,正四面体 的棱长为4,
的棱长为4,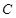 在平面
在平面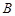 是直线
是直线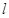 上的动点,则当
上的动点,则当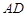 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面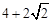

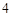
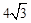
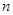 个点最多将直线分成
个点最多将直线分成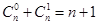 段,平面上
段,平面上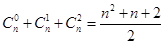 部分(规定:若
部分(规定:若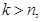 则
则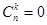 ),则类似地可以推算得到空间里
),则类似地可以推算得到空间里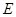 、
、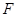 、
、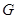 、
、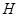 分别是正方体
分别是正方体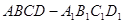 的棱
的棱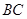 、
、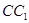 、
、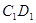 、
、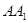 的中点。
的中点。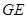 ∥平面
∥平面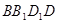 ;
;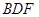 ∥平面
∥平面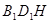
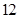 的正方形
的正方形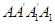 中,
中,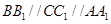 ,且
,且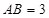 ,
,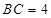 ,
,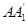 分别交
分别交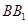 、
、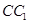 于
于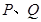 两点, 将正方形沿
两点, 将正方形沿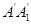 与
与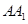 重合,
重合,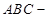
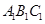 .
. 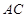 上有一点
上有一点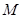 ,且
,且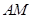 :
: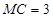 :
: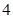 , 求证:
, 求证: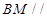 平面
平面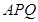 ;
; 与平面
与平面 所成角的正弦值
所成角的正弦值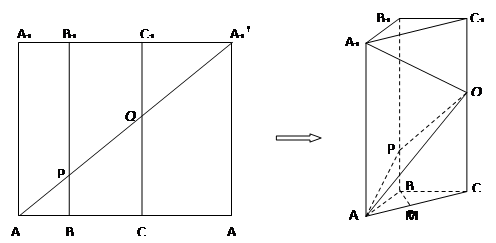
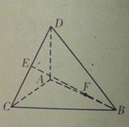
 平面ABC,
平面ABC, ,AC=CB=AD=2,E是DC的中点,F是AB的中点。
,AC=CB=AD=2,E是DC的中点,F是AB的中点。 ;
;
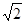 的四棱锥
的四棱锥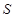 -
- 的底面是边长为1的正方形,点
的底面是边长为1的正方形,点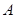 、
、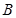 、
、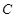 、
、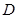 均在半径为1的同一球面上,则底面
均在半径为1的同一球面上,则底面