题目内容
已知直线上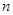
个点最多将直线分成
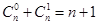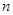段，平面上条直线最多将平面分成
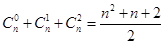部分（规定：若
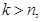则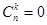
），则类似地可以推算得到空间里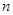个平面最多将空间分成 ▲ 部分
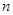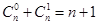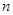个点最多将直线分成段，平面上条直线最多将平面分成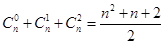部分（规定：若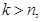则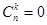），则类似地可以推算得到空间里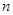个平面最多将空间分成 ▲ 部分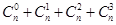
这里推理依次为一维，二维，三维等情况，根据已有结论的构成，可以推算得到空间里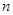个平面最多将空间分成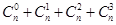部分。
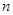个平面最多将空间分成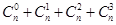部分。
练习册系列答案
相关题目
题目内容
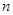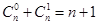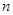个点最多将直线分成段，平面上条直线最多将平面分成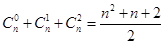部分（规定：若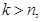则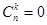），则类似地可以推算得到空间里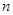个平面最多将空间分成 ▲ 部分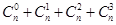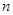个平面最多将空间分成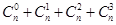部分。
中，平面
平面
，平面
平面
为
上任意一点，
为菱形
平面
；
，三棱锥
的体积是四棱锥
，二面角
的大小为
，求
,底面
为正三角形，
平面
,
,
为
中点.
平面
；
与平面
两个不重合的平面
，给出下列四个命题： 
则
；
且
则
；
则
则
. 其中真命题是 （ ）
的球的内接正方体的棱长为_____________。
中，
⊥底面
，
∥
，
⊥平面
；
的平面角的余弦值；
到平面
的距离。
中，
，
，
为
中点．将
沿
折起至
，使得平面
平面
，
分别为
的中点．
面
;
的余弦值．
底面ABCD，E是PC的中点．
，
，求三棱锥P-BDE的体积。
