题目内容
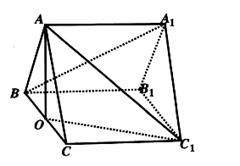
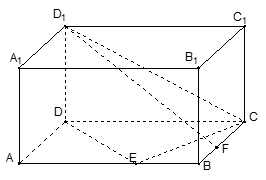
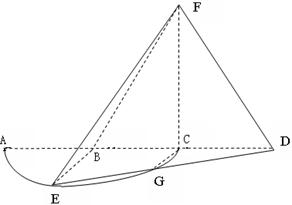
如右下图,在长方体ABCD—A1B1C1D1中,已知AB=" 4," AD ="3," AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C—DE—C1的余弦值;
(2) 求直线EC1与FD1所成的余弦值.
(1) 求二面角C—DE—C1的余弦值;
(2) 求直线EC1与FD1所成的余弦值.

解:(I)(法一)矩形ABCD中过C作CH DE于H,连结C1H
DE于H,连结C1H
 CC1
CC1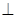 面ABCD,CH为C1H在面ABCD上的射影
面ABCD,CH为C1H在面ABCD上的射影
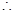 C1H
C1H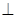 DE
DE 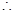
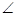 C1HC为二面角C—DE—C1的平面角
C1HC为二面角C—DE—C1的平面角
矩形ABCD中得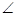 EDC=
EDC= ,
,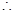
 DCH中得CH=
DCH中得CH= ,
,
又CC1=2,
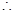
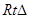 C1HC中,
C1HC中,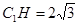 ,
,
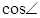 C1HC
C1HC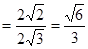
 二面角C—DE—C1的余弦值为
二面角C—DE—C1的余弦值为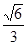 7分
7分
(2)以D为原点,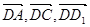 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
设EC1与FD1所成角为β,则
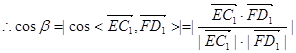
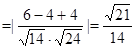
故EC1与FD1所成角的余弦值为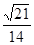 14分
14分
(法二)(1)以D为原点,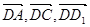 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
于是,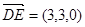 ,
,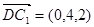 ,
,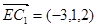
设向量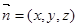 与平面C1DE垂直,则有
与平面C1DE垂直,则有
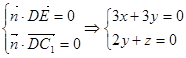 ,
,
令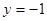 ,则
,则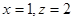
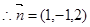
又面CDE的法向量为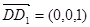
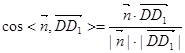
 7分
7分
由图,二面角C—DE—C1为锐角,故二面角C—DE—C1的余弦值为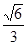 8分
8分
(II)设EC1与FD1所成角为β,则
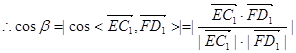
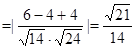
故EC1与FD1所成角的余弦值为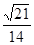 14分
14分
 DE于H,连结C1H
DE于H,连结C1H CC1
CC1 面ABCD,CH为C1H在面ABCD上的射影
面ABCD,CH为C1H在面ABCD上的射影 C1H
C1H DE
DE 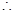
 C1HC为二面角C—DE—C1的平面角
C1HC为二面角C—DE—C1的平面角矩形ABCD中得
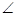 EDC=
EDC= ,
,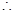
 DCH中得CH=
DCH中得CH= ,
,又CC1=2,
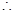
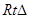 C1HC中,
C1HC中,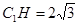 ,
,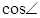 C1HC
C1HC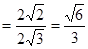
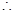 二面角C—DE—C1的余弦值为
二面角C—DE—C1的余弦值为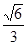 7分
7分(2)以D为原点,
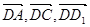 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)设EC1与FD1所成角为β,则

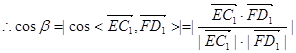
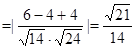
故EC1与FD1所成角的余弦值为
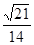 14分
14分(法二)(1)以D为原点,
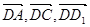 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)于是,
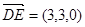 ,
,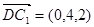 ,
,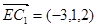
设向量
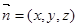 与平面C1DE垂直,则有
与平面C1DE垂直,则有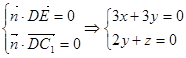 ,
,令
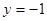 ,则
,则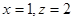
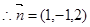
又面CDE的法向量为
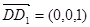
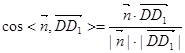
 7分
7分由图,二面角C—DE—C1为锐角,故二面角C—DE—C1的余弦值为
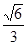 8分
8分(II)设EC1与FD1所成角为β,则

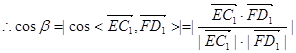
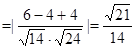
故EC1与FD1所成角的余弦值为
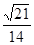 14分
14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
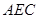 是半径为
是半径为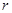 的半圆,
的半圆,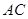 为直径,点
为直径,点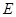 为弧
为弧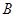 和点
和点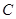 为线段
为线段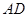 的三等分点,线段
的三等分点,线段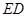 与弧
与弧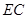 交于点
交于点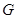 ,且
,且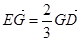 ,平面
,平面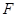 满足
满足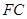
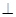 平面
平面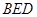 ,
,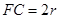 。
。
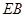
 ;
; (及其内部)绕
(及其内部)绕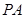 垂直平行四边形
垂直平行四边形 所在平面,若
所在平面,若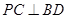 ,则平行则四边形
,则平行则四边形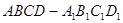 中,
中,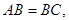
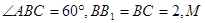 为
为 中点,点
中点,点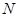 在
在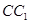 上。(1)试确定点
上。(1)试确定点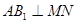 ;(2)当
;(2)当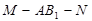 的正切值。
的正切值。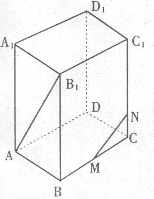
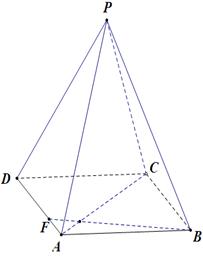
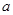 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=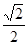 AD.
AD.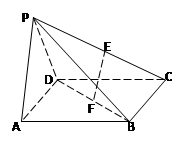
 中,AB=1,侧棱
中,AB=1,侧棱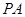 与底面
与底面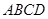 所成角的正切值为
所成角的正切值为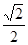 .
.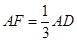 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.
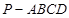 中,平面
中,平面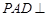 平面
平面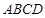 ,平面
,平面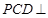 平面
平面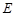 为
为 上任意一点,
上任意一点,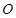 为菱形
为菱形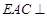 平面
平面 ;
;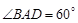 ,三棱锥
,三棱锥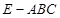 的体积是四棱锥
的体积是四棱锥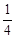 ,二面角
,二面角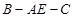 的大小为
的大小为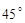 ,求
,求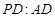

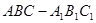 ,底面
,底面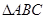 为正三角形,
为正三角形,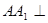 平面
平面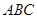
 ,
,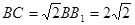 ,
,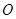 为
为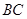 中点.
中点.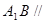 平面
平面 ;
; 与平面
与平面