题目内容
【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
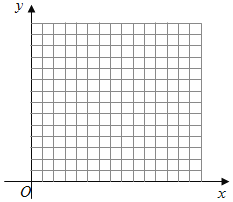
,第5组![]() ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。

(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
【答案】(1)0.1;(2)第3、4、5组分别抽取3人、2人、1人;(3)![]() .
.
【解析】
本试题主要是考查了直方图的性质的运用,以及古典概型概率的运算的综合运用。
(1)由题设可知,第![]() 组的频率为
组的频率为![]() 第
第![]() 组的频率为
组的频率为![]()
第![]() 组的频率为
组的频率为![]() 。
。
(2)第![]() 组的人数为
组的人数为![]() 第
第![]() 组的人数为
组的人数为![]()
第![]() 组的人数为
组的人数为![]() 。利用分层抽样的等比例性质得到各层应该抽取的人数。
。利用分层抽样的等比例性质得到各层应该抽取的人数。
(3)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,则从六位同学中抽两位同学有15中情况,其中其中第
,则从六位同学中抽两位同学有15中情况,其中其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有其中第
至少有一位同学入选的有其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有9种,进而得到概率值。
至少有一位同学入选的有9种,进而得到概率值。
解:(Ⅰ)由题设可知,第![]() 组的频率为
组的频率为![]() 第
第![]() 组的频率为
组的频率为![]()
第![]() 组的频率为
组的频率为![]() 。 ……………………………………………………3分
。 ……………………………………………………3分
(Ⅱ)第![]() 组的人数为
组的人数为![]() 第
第![]() 组的人数为
组的人数为![]()
第![]() 组的人数为
组的人数为![]() 。 ……………………………………………………6分
。 ……………………………………………………6分
因为第![]() 组共有
组共有![]() 名学生,所以利用分层抽样在
名学生,所以利用分层抽样在![]() 名学生中抽取
名学生中抽取![]() 名学生,每组抽取的人数分别为: 第
名学生,每组抽取的人数分别为: 第![]() 组:
组:![]() 第
第![]() 组:
组:![]() 第
第![]() 组:
组:![]()
所以第![]() 组分别抽取
组分别抽取![]() 人、
人、![]() 人、
人、![]() 人 …………………………………………9分
人 …………………………………………9分
(Ⅲ)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,则从六位同学中抽两位同学有:
,则从六位同学中抽两位同学有:![]()
![]()
![]()
共![]() 种可能。 ……………………………………………10分
种可能。 ……………………………………………10分
其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有:
至少有一位同学入选的有:![]()
![]() 共
共![]() 种可能, ……………………11分
种可能, ……………………11分
所以第![]() 组至少有一名学生被甲考官面试的概率为
组至少有一名学生被甲考官面试的概率为![]() …………………12分
…………………12分