题目内容
在棱长为1的正方体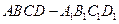 中,
中,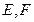 分别是
分别是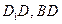 的中点,
的中点,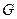 在棱
在棱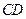 上,且
上,且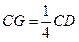 ,H
,H 为
为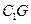 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.
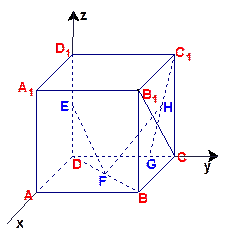
(1)求证: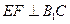 ;
;
(2)求EF与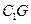 所成的角的余弦;
所成的角的余弦;
(3)求FH的长.
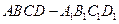 中,
中,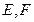 分别是
分别是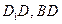 的中点,
的中点,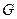 在棱
在棱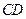 上,且
上,且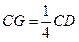 ,H
,H 为
为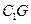 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.
(1)求证:
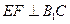 ;
;(2)求EF与
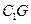 所成的角的余弦;
所成的角的余弦;(3)求FH的长.
略
略

练习册系列答案
相关题目
题目内容
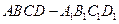 中,
中,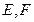 分别是
分别是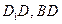 的中点,
的中点,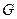 在棱
在棱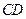 上,且
上,且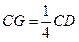 ,H
,H 为
为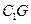 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.
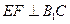 ;
;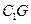 所成的角的余弦;
所成的角的余弦;