题目内容
在
四面体
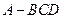中,共顶点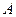
的三条棱两两互相垂直,且
，
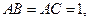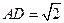若四
面体的四个顶点在一个球面上,则B，D的球面距离为_ ___ __。 
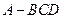四面体中,共顶点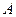的三条棱两两互相垂直,且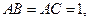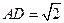，若四面体的四个顶点在一个球面上,则B，D的球面距离为_ ___ __。 
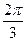
略
练习册系列答案
小学期末标准试卷系列答案
相关题目
小学期末标准试卷系列答案题目内容
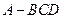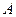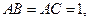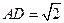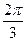
四面体中,共顶点的三条棱两两互相垂直,且，若四面体的四个顶点在一个球面上,则B，D的球面距离为_ ___ __。 小学期末标准试卷系列答案
和
三棱锥
组合而成，点
、
、
在圆
的圆周上，其正（主）视图、侧（左）视图的面积分别为10和12，如图所示，其中
，
，
，
．
；
的平面角的大小．
，
，
两两互相垂直，点
∈
，点
是
倍，则点
中，
，
是侧棱
的中点.
；
的大小.
的底面为直角梯形，
，
底面
，且
，
，
是
的中点。
面
；
与
与面
所成二面角的余弦值.
中，
分别是
的中点，
在棱
上，且
，H
为
的中点，应用空间向量方法求解下列问题.
;
平面ABC，则点P到BC的距离是（ ）