题目内容
如图,PA垂直于矩形ABCD所在的平面,PD=PA,E、F分别是AB、PD的中点。
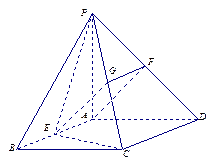
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD。

(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD。
见解析
(1)取PC中点G,连接FG、EG。
因为F、G分别为PD、PC的中点,
所以FG∥CD且FG=CD,
又AE∥CD且AE=CD,
所以,FG∥AE且FG=AE,
四边形AEGF为平行四边形,
因此,AF∥EG,又AF?平面PCE,所以AF∥平面PCE。
(2) 由PA⊥平面ABCD,知PA⊥CD,
又CD⊥AD,所以CD⊥平面PAD,CD⊥AF。
又PA⊥AD,F为PD的中点,则AF⊥PD,
因此,AF⊥平面PCD。
而AF∥EG,故EG⊥平面PCD,
又EG?平面PCE,所以,平面PCE⊥平面PCD。
因为F、G分别为PD、PC的中点,
所以FG∥CD且FG=CD,
又AE∥CD且AE=CD,
所以,FG∥AE且FG=AE,
四边形AEGF为平行四边形,
因此,AF∥EG,又AF?平面PCE,所以AF∥平面PCE。
(2) 由PA⊥平面ABCD,知PA⊥CD,
又CD⊥AD,所以CD⊥平面PAD,CD⊥AF。
又PA⊥AD,F为PD的中点,则AF⊥PD,
因此,AF⊥平面PCD。
而AF∥EG,故EG⊥平面PCD,
又EG?平面PCE,所以,平面PCE⊥平面PCD。

练习册系列答案
相关题目
 截一球面得圆
截一球面得圆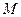 ,过圆心
,过圆心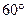 二面角的平面
二面角的平面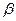 截该球面得圆
截该球面得圆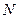 ,若该球面的半径为4,圆
,若该球面的半径为4,圆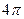 ,则圆
,则圆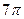 (B)
(B)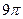 (c)
(c)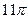 (D)
(D)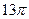
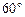 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.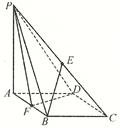
 和
和 三棱锥
三棱锥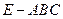 组合而成,点
组合而成,点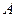 、
、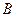 、
、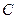 在圆
在圆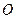 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中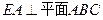 ,
,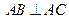 ,
,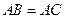 ,
,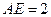 .
.
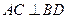 ;
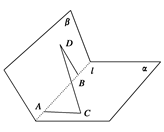
;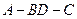 的平面角的大小.
的平面角的大小.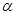 ,
,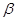 ,
,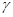 两两互相垂直,点
两两互相垂直,点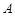 ∈
∈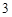 ,点
,点 是
是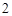 倍,则点
倍,则点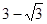
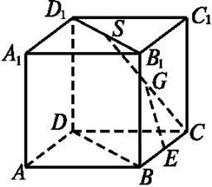
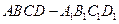 中,
中,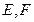 分别是
分别是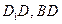 的中点,
的中点,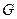 在棱
在棱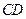 上,且
上,且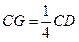 ,H
,H 为
为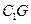 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.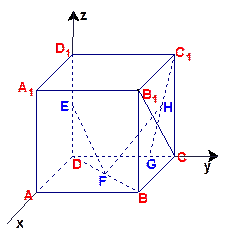
 ;
;