题目内容
11.在△ABC中,角A,B,C所对的边分别是a,b,c,若向量$\overrightarrow{p}$=(4,a2+b2-c2),$\overrightarrow{q}$=($\sqrt{3}$,$\frac{1}{2}$absinC),且满足$\overrightarrow{p}$∥$\overrightarrow{q}$,则C=( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 通过向量的平行的坐标运算,求出S的表达式,利用余弦定理以及三角形面积,求出C的正切值,得到C的值即可.
解答 解:由$\overrightarrow{p}$∥$\overrightarrow{q}$,得4×$\frac{1}{2}$absinC=$\sqrt{3}$(a2+b2-c2),则2absinC=$\sqrt{3}$(a2+b2-c2).
由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
所以2absinC=$\sqrt{3}$×2abcosC,
解得:tanC=$\sqrt{3}$.又C∈(0,180°),
所以C=60°.
故选:C.
点评 本题考查向量的平行,三角形的面积公式以及余弦定理的应用,考查计算能力,属于基本知识的考查.

练习册系列答案
相关题目
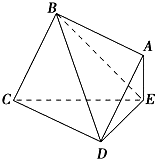 正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.
正方形ABCD所在的平面与三角形CDE所在的平面交于CD,且AE⊥平面CDE.