题目内容
17.计算:(1)求$y=\sqrt{x}-sin\frac{x}{2}cos\frac{x}{2}+{e^{-x}}$的导数.
(2)$\int_{-3}^1{|{{x^2}-4}|dx}$=$\frac{34}{3}$.
分析 (1)根据求导公式和法则求出已知函数的导数即可.
(2)根据定积分的计算方法计算即可,
解答 解(1):∵$y=\sqrt{x}-\frac{1}{2}sinx+{e^{-x}}∴y'=\frac{1}{{2\sqrt{x}}}-\frac{1}{2}cosx-{e^{-x}}$
(2):原式=$\int_{-3}^{-2}{({x^2}-4)dx+\int_{-2}^1{(4-{x^2})dx}}$=($\frac{1}{3}$x3-4x)|${\;}_{-3}^{-2}$+(4x-$\frac{1}{3}$x3)|${\;}_{-2}^{1}$=$\frac{34}{3}$.
故答案为:$\frac{34}{3}$.
点评 本题考查了求导公式和法则和定积分的计算,是基础题.

练习册系列答案
相关题目
12.己知向量$\overrightarrow a$,$\overrightarrow b$非零不共线,则下列各组向量中,可作为平面向量的一组基底的是( )
| A. | $\overrightarrow a+\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$,$\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$,$2\overrightarrow a+\overrightarrow b$ | D. | $2\overrightarrow a-2\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ |
2.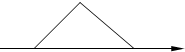 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
9. 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
6.设集合A={(x,y)||x|+|y|≤1},若动点P(x,y)∈A,则x2+(y-1)2≤2的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
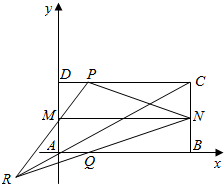 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),