题目内容
20.当实数m取何值时,复数z1=(m+1)+(m-6)i分别是实数、虚数、纯虚数.分析 利用复数的概念可求当实数m取什么数值时,复数z=m+1+(m-1)i分别是实数,虚数,纯虚数.
解答 解:(1)当m-6=0,即m=6时,复数z是实数;
(2)当m-6≠0,即m≠6时,复数z是虚数;
(3)当m+1=0,且m-6≠0时,即m=-1时,复数z是纯虚数.
点评 本题考查复数的概念,属于基础题.

练习册系列答案
相关题目
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}=1$的离心率为2,则此双曲线的顶点到渐近线的距离等于( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
12.己知向量$\overrightarrow a$,$\overrightarrow b$非零不共线,则下列各组向量中,可作为平面向量的一组基底的是( )
| A. | $\overrightarrow a+\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$,$\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$,$2\overrightarrow a+\overrightarrow b$ | D. | $2\overrightarrow a-2\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ |
9.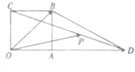 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
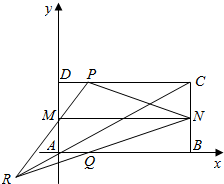 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),