题目内容
10.“条件甲:$\frac{1}{4}≤{2^a}≤\frac{1}{2}$”是“条件乙:(a+1)(a+2)≤1”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 先解条件甲、乙中的不等式,从而得到条件甲:-2≤a≤-1,条件乙:$\frac{-3-\sqrt{5}}{2}≤a≤\frac{-3+\sqrt{5}}{2}$,通过作差即可比较出-2和$\frac{-3-\sqrt{5}}{2}$,-1和$\frac{-3+\sqrt{5}}{2}$的大小关系,从而判断出条件甲是乙的什么条件.
解答 解:通过解不等式得到:
条件甲:-2≤a≤-1;
条件乙:$\frac{-3-\sqrt{5}}{2}≤a≤\frac{-3+\sqrt{5}}{2}$;
∵$\frac{-3-\sqrt{5}}{2}<-2,\frac{-3+\sqrt{5}}{2}>-1$;
∴条件甲成立能得到条件乙成立,而条件乙成立得不到条件甲成立;
∴条件甲是条件乙的充分不必要条件.
故选A.
点评 考查指数函数的单调性,根据单调性解不等式的方法,以及解一元二次不等式,充分条件、必要条件,及充分不必要条件的概念.

练习册系列答案
相关题目
1.方程x2+y2+ax+2ay+2a2+a-1=0表示的曲线是圆,则a的取值范围是( )
| A. | R | B. | (-∞,-2)∪($\frac{2}{3}$,+∞) | C. | (-$\frac{2}{3}$,2) | D. | (-2,$\frac{2}{3}$) |
15.在△ABC中,若c2+ab=a2+b2,则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
2.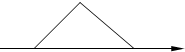 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
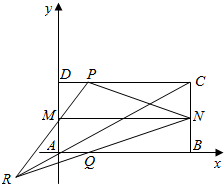 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),