题目内容
15.二项式(2x-$\frac{1}{x}$)5的展开式中含$\frac{1}{x}$项的系数为-40.分析 根据二项式展开式的通项公式,即可求出展开式中含$\frac{1}{x}$项的系数.
解答 解:二项式(2x-$\frac{1}{x}$)5的展开式的通项公式为
Tr+1=${C}_{5}^{r}$•(2x)5-r•${(-\frac{1}{x})}^{r}$
=(-1)r•${C}_{5}^{r}$•25-r•x5-2r,
令5-2r=-1,
解得r=3;
∴展开式中含$\frac{1}{x}$项的系数为
(-1)3•${C}_{5}^{3}$•25-3=-40.
故答案为:-40.
点评 本题考查了二项式定理的应用问题,也考查了二项式展开式的通项公式的应用问题,是基础题目.

练习册系列答案
相关题目
6.已知点P(tanα,cosα)在第三象限,则角α的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.过曲线S:y=3x-x3上一点A(2,-2)的切线方程为( )
| A. | y=-2 | B. | 9x+y-16=0 | C. | 9x+y-16=0或y=-2 | D. | 9x-y-16=0 |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}=1$的离心率为2,则此双曲线的顶点到渐近线的距离等于( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
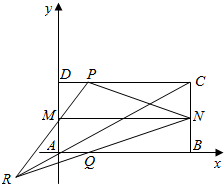 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),