题目内容
设椭圆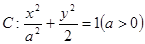 的左、右顶点分别为
的左、右顶点分别为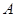 、
、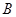 ,点
,点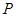 在椭圆上且异于
在椭圆上且异于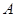 、
、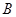 两点,
两点,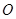 为坐标原点.
为坐标原点.
(1)若直线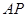 与
与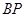 的斜率之积为
的斜率之积为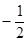 ,求椭圆的离心率;
,求椭圆的离心率;
(2)对于由(1)得到的椭圆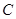 ,过点
,过点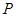 的直线
的直线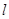 交
交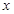 轴于点
轴于点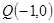 ,交
,交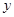 轴于点
轴于点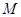 ,若
,若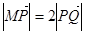 ,求直线
,求直线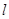 的斜率.
的斜率.
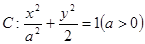 的左、右顶点分别为
的左、右顶点分别为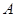 、
、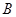 ,点
,点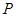 在椭圆上且异于
在椭圆上且异于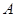 、
、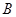 两点,
两点,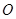 为坐标原点.
为坐标原点.(1)若直线
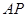 与
与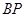 的斜率之积为
的斜率之积为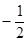 ,求椭圆的离心率;
,求椭圆的离心率;(2)对于由(1)得到的椭圆
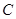 ,过点
,过点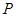 的直线
的直线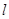 交
交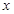 轴于点
轴于点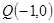 ,交
,交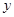 轴于点
轴于点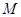 ,若
,若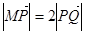 ,求直线
,求直线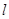 的斜率.
的斜率. (1) 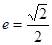 .
.
(2)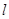 的斜率
的斜率 .
.
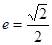 .
.(2)
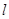 的斜率
的斜率 .
.试题分析:(1)先求出A,B的坐标,然后利用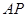 与
与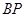 的斜率之积为
的斜率之积为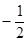 ,建立关于a的方程,从而求出a值,进一步可求出椭圆的离心率.
,建立关于a的方程,从而求出a值,进一步可求出椭圆的离心率.
(2)设直线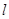 的斜率为
的斜率为 , 直线
, 直线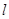 的方程为
的方程为 ,则有
,则有 ,
,
设 ,由于
,由于 三点共线,且
三点共线,且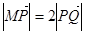 ,
,
再把此条件坐标可知 ,从而得到
,从而得到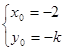 或
或 ,
,
再利用点P在椭圆上,可建立关于k的方程求出k的值.
解:(1) 由已知 ,设
,设 . …………1分
. …………1分
则直线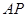 的斜率
的斜率 ,
,
直线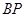 的斜率
的斜率 .
.
由 ,得
,得 . …………2分
. …………2分

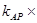


 …………3分
…………3分
 ,得
,得 , …………4分
, …………4分

 . …………5分
. …………5分
 椭圆的离心率
椭圆的离心率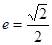 . …………6分
. …………6分
(2) 由题意知直线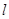 的斜率存在. …………7分
的斜率存在. …………7分
设直线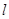 的斜率为
的斜率为 , 直线
, 直线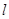 的方程为
的方程为 …………8分
…………8分
则有 ,
,
设 ,由于
,由于 三点共线,且
三点共线,且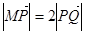
根据题意,得 …………9分
…………9分
解得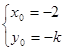 或
或 …………11分
…………11分
又点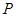 在椭圆上,又由(1)知椭圆
在椭圆上,又由(1)知椭圆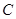 的方程为
的方程为
所以 …………①
…………①
或 …………②
…………②
由①解得 ,即
,即 ,
,
 此时点
此时点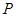 与椭圆左端点
与椭圆左端点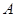 重合,
重合,  舍去; …………12分
舍去; …………12分
由②解得 ,即
,即 …………13分
…………13分
 直线直线
直线直线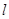 的斜率
的斜率 . …………14分
. …………14分
点评:两点 的斜率公式
的斜率公式 ;另外解本小题的关键是条件
;另外解本小题的关键是条件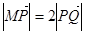 的使用,实际上此条件是用k表示出点P的坐标,再根据点P在椭圆上,建立关于k的方程求出k值.
的使用,实际上此条件是用k表示出点P的坐标,再根据点P在椭圆上,建立关于k的方程求出k值.
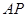 与
与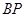 的斜率之积为
的斜率之积为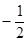 ,建立关于a的方程,从而求出a值,进一步可求出椭圆的离心率.
,建立关于a的方程,从而求出a值,进一步可求出椭圆的离心率.(2)设直线
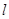 的斜率为
的斜率为 , 直线
, 直线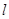 的方程为
的方程为 ,则有
,则有 ,
,设
 ,由于
,由于 三点共线,且
三点共线,且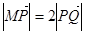 ,
,再把此条件坐标可知
 ,从而得到
,从而得到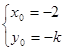 或
或 ,
,再利用点P在椭圆上,可建立关于k的方程求出k的值.
解:(1) 由已知
 ,设
,设 . …………1分
. …………1分则直线
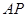 的斜率
的斜率 ,
,直线
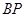 的斜率
的斜率 .
.由
 ,得
,得 . …………2分
. …………2分
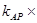


 …………3分
…………3分 ,得
,得 , …………4分
, …………4分
 . …………5分
. …………5分 椭圆的离心率
椭圆的离心率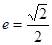 . …………6分
. …………6分(2) 由题意知直线
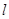 的斜率存在. …………7分
的斜率存在. …………7分设直线
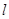 的斜率为
的斜率为 , 直线
, 直线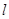 的方程为
的方程为 …………8分
…………8分则有
 ,
,设
 ,由于
,由于 三点共线,且
三点共线,且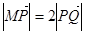
根据题意,得
 …………9分
…………9分解得
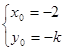 或
或 …………11分
…………11分又点
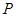 在椭圆上,又由(1)知椭圆
在椭圆上,又由(1)知椭圆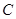 的方程为
的方程为
所以
 …………①
…………①或
 …………②
…………②由①解得
 ,即
,即 ,
, 此时点
此时点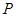 与椭圆左端点
与椭圆左端点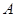 重合,
重合,  舍去; …………12分
舍去; …………12分由②解得
 ,即
,即 …………13分
…………13分 直线直线
直线直线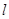 的斜率
的斜率 . …………14分
. …………14分点评:两点
 的斜率公式
的斜率公式 ;另外解本小题的关键是条件
;另外解本小题的关键是条件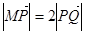 的使用,实际上此条件是用k表示出点P的坐标,再根据点P在椭圆上,建立关于k的方程求出k值.
的使用,实际上此条件是用k表示出点P的坐标,再根据点P在椭圆上,建立关于k的方程求出k值.
练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )



 与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为 

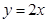 ,焦距为
,焦距为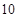 ,这双曲线的方程为___
,这双曲线的方程为___  时的椭圆的标准方程是 .
时的椭圆的标准方程是 . 的准线方程是( ).
的准线方程是( ).



 为椭圆
为椭圆 的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为 为线段
为线段 的中点,则
的中点,则 ( )
( ) 内有一动点
内有一动点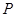 ,已知
,已知 ,且满足
,且满足 ,求
,求 、
、 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则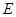 的离心率为( )
的离心率为( )


