题目内容
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: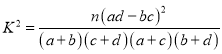 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)见解析;(2)![]() ;(3)有把握.
;(3)有把握.
【解析】
(1)由表可依次求出男性不辅导的人数、女性辅导的人数、不辅导的人数、女性的人数、女性不辅导的人数,由此得到答案;
(2)根据频率的计算公式求解即可;
(3)求出![]() ,然后与
,然后与![]() 比较大小,由此可求得结论.
比较大小,由此可求得结论.
解:(1)如表,
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 35 | 60 |
女 | 15 | 5 | 20 |
合计 | 40 | 40 | 80 |
(2)在样本中有20位女士,其中有15位辅导孩子作业,其频率为![]() ,
,
∴估计成人女士晚上八点至十点辅导孩子作业的概率为![]() ;
;
(3)∵![]()
![]() ,
,
∴有99%的把握认为“晚上八点至十点时间是否段辅导孩子作业与性别有关”.

【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?