题目内容
【题目】已知数列{an}的前n项和为Sn,且Sn＝n（n+2）（n∈N*）.
（1）求数列{an}的通项公式；
（2）设bn
,求数列{bn}的前n项和Tn.
【答案】（1）an＝2n+1；（2）Tn
.
【解析】
（1）由n＝1时求得a1,当n≥2时,由Sn＝n（n+2）（n∈N*）① ,
可得Sn﹣1＝（n﹣1）（n+1）② ,由①﹣②得an＝2n+1,再检验当n＝1时是否适合,求得an；
（2）由（1）求得bn
,再利用错位相减法求其前n项和Tn即可.
解：（1）由题知：当n＝1时,有S1＝1×3＝3＝a1；
当n≥2时,由Sn＝n（n+2）（n∈N*）① ,
可得Sn﹣1＝
② ,由①﹣② 得an＝2n+1,
又n＝1时也适合,故an＝2n+1；
（2）由（1）知bn,
∵Tn＝3
5
7×（
）3+…+（2n+1）（）n③,
∴
35×（）3+…+（2n+1）
④,
由③﹣④可得：
,
所以Tn.
【题目】某校举行了全体学生的一分钟跳绳比赛，为了了解学生的体质，随机抽取了100名学生，其跳绳个数的频数分布表如下：
一分钟跳绳个数 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 18 | 30 | 16 | 10 | 8 |
（1）若将抽取的100名学生一分钟跳绳个数作为一个样本，请将这100名学生一分钟跳绳个数的频率分布直方图补充完整（只画图，不需要写出计算过程）；
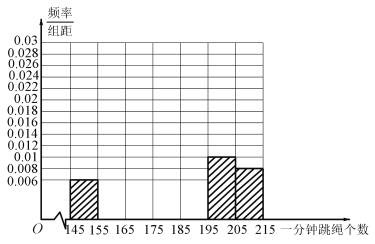
（2）若该校共有3000名学生，所有学生的一分钟跳绳个数X近似服从正态分布
，其中
为样本平均数的估计值（同一组中的数据用该组区间的中点值为代表）.利用所得正态分布模型，解决以下问题：
①估计该校一分钟跳绳个数超过165个的人数（结果四舍五入到整数）；
②若在该校所有学生中任意抽取4人，设一分钟跳绳个数超过180个的人数为
，求随机变量的分布列、期望与方差./span>
附：若随机变量Z服从正态分布
，则
，
，
.
【题目】随机调查某城市80名有子女在读小学的成年人，以研究晚上八点至十点时间段辅导子女作业与性别的关系，得到下面的数据表：
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
（1）请将表中数据补充完整；
（2）用样本的频率估计总体的概率，估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率；
（3）根据以上数据，能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关？”.
参考公式：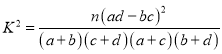
，其中
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
