题目内容
15．计算：（C${\;}_{15}^{0}$）2+（C${\;}_{15}^{1}$）2+（C${\;}_{15}^{2}$）2+…+（C${\;}_{15}^{15}$）2．分析 由（1+x）15•（1+x）15=（1+x）30，在展开式中比较x15系数即可求解．
解答 解：（1+x）15•（1+x）15=（1+x）30，
∴$（{C}_{15}^{0}+{C}_{15}^{1}x+…+{C}_{15}^{15}{x}^{15}）$•$（{C}_{15}^{0}+{C}_{15}^{1}x+…+{C}_{15}^{15}{x}^{15}）$=$（{C}_{30}^{0}+{C}_{30}^{1}x+…+{C}_{30}^{30}{x}^{30}）$，
比较x15系数可得，${C}_{15}^{0}{C}_{15}^{15}$$+{C}_{15}^{1}{C}_{15}^{14}+{C}_{15}^{2}{C}_{15}^{13}+…+{C}_{15}^{15}{C}_{15}^{0}$=${C}_{30}^{15}$，
∴（C${\;}_{15}^{0}$）2+（C${\;}_{15}^{1}$）2+（C${\;}_{15}^{2}$）2+…+（C${\;}_{15}^{15}$）2=${C}_{30}^{15}$．
点评 本题主要考查了二项展开式的应用，解题关键是根据已知式子构造展开式中指定项的系数．
练习册系列答案
相关题目
5．已知某个车轮旋转的角度α（弧度）与时间t（秒）的函数关系是α=$\frac{2π}{0.64}$t2（t≥0），则车轮启动后第1.6秒时的瞬时角速度是（ ）
| A． | 20π弧度/秒 | B． | 10π弧度/秒 | C． | 8π弧度/秒 | D． | 5π弧度/秒 |
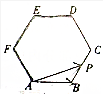如图所示，点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动，其中AB=k，则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$，0]∪[k，$\frac{3}{2}{k}^{2}$]．