题目内容
7.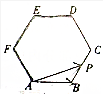 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
分析 连接AE,可分别以直线AB,AE为x,y轴,建立平面直角坐标系,可得到$\overrightarrow{AB}=(k,0)$,设P(x,y),P点在AB或DE上时,0≤x≤k,并求出$\overrightarrow{AP}•\overrightarrow{AB}=x$,从而得出对应的$\overrightarrow{AP}•\overrightarrow{AB}$的取值范围,讨论P点在其它边上时用y表示x,并写出y的范围,从而可得到对应的$\overrightarrow{AP}•\overrightarrow{AB}$的取值范围,最后对以上求出的$\overrightarrow{AP}•\overrightarrow{AB}$取值范围求并集即可.
解答 解:连接AE,则AE⊥AB;
∴分别以直线AB,AE为x,y轴,建立如图所示平面直角坐标系: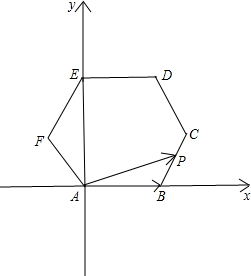 $\overrightarrow{AB}=(k,0)$,设$\overrightarrow{AP}=(x,y)$;
$\overrightarrow{AB}=(k,0)$,设$\overrightarrow{AP}=(x,y)$;
(1)若P点在边AB上时,y=0,0≤x≤k,∴P(x,0);
∴$\overrightarrow{AP}•\overrightarrow{AB}=kx$,k≤kx≤k2;
∴$k≤\overrightarrow{AP}•\overrightarrow{AB}≤{k}^{2}$;
(2)若P在边BC上,x=$\frac{\sqrt{3}}{3}y+k$,$0≤y≤\frac{\sqrt{3}}{2}k$,∴P$(\frac{\sqrt{3}}{3}y+k,y)$;
∴$\overrightarrow{AP}•\overrightarrow{AB}=\frac{\sqrt{3}}{3}ky+{k}^{2}$;
∴${k}^{2}≤\overrightarrow{AP}•\overrightarrow{AB}≤\frac{3}{2}{k}^{2}$;
(3)若P在边CD上,$x=\frac{3}{2}k-\frac{\sqrt{3}}{3}y$,$0≤y≤\frac{\sqrt{3}}{2}k$,∴P($\frac{3}{2}k-\frac{\sqrt{3}}{3}y,y$);
∴$\overrightarrow{AP}•\overrightarrow{AB}=\frac{3}{2}{k}^{2}-\frac{\sqrt{3}}{3}ky$;
∴${k}^{2}≤\overrightarrow{AP}•\overrightarrow{AB}≤\frac{3}{2}{k}^{2}$;
(4)若P在边DE上,0≤x≤k,P(x,y);
∴$\overrightarrow{AP}•\overrightarrow{AB}=x$;
∴$0≤\overrightarrow{AP}•\overrightarrow{AB}≤k$;
(5)若P在边EF或FA上,$-\frac{k}{2}≤x≤0$,P(x,y);
∴$\overrightarrow{AP}•\overrightarrow{AB}=x$;
∴$-\frac{k}{2}≤\overrightarrow{AP}•\overrightarrow{AB}≤0$;
综上得$\overrightarrow{AP}•\overrightarrow{AB}$的取值区间为[$-\frac{k}{2},0$]∪[$k,\frac{3}{2}{k}^{2}$].
故答案为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
点评 考查正六边形的定义,正六边形的内角,以及通过建立平面直角坐标系,利用向量的坐标计算数量积的方法,能够想到讨论P点在每一边上时数量积的范围,数量积的坐标运算.

| A. | {x|0≤x≤2} | B. | {x|1≤x≤2} | C. | {x|0≤x≤4} | D. | {x|1≤x≤4} |
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (1,3) | D. | (3,+∞) |