题目内容
6.设平面向量组ai (i=1,2,3,…)满足:①|ai|=1;②ai•ai+1=0,设Tn=|a1+a2+…+an|(n≥2),则T4的最大值为$2\sqrt{2}$.分析 由已知条件,可用有向线段表示出T4取最大值时的向量$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+\overrightarrow{{a}_{3}}+\overrightarrow{{a}_{4}}$,由图形即可求出T4的最大值.
解答 解:根据已知条件向量$\overrightarrow{{a}_{i}}$的长度为1,相邻向量$\overrightarrow{{a}_{i}}⊥\overrightarrow{{a}_{i+1}}$,i=1,2,3,…;
${T}_{4}=|\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+\overrightarrow{{a}_{3}}+\overrightarrow{{a}_{4}}|$;
用有向线段表示出T4取最大值时的向量$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+\overrightarrow{{a}_{3}}+\overrightarrow{{a}_{4}}$如下图: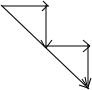 显然T4的最大值为$2\sqrt{2}$.
显然T4的最大值为$2\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 考查向量长度的概念,两非零向量垂直的充要条件,以及用有向线段表示向量,向量加法的几何意义.

练习册系列答案
相关题目
17.设集合A=[-1,2],B={x|1≤x≤4},则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|1≤x≤2} | C. | {x|0≤x≤4} | D. | {x|1≤x≤4} |
16.已知函数f(x)=|x-2|+1,g(x)=loga(x+1)(a>0,且a≠1),若函数f(x)-g(x)有两个不相同的零点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (1,3) | D. | (3,+∞) |
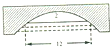 一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.
一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.