题目内容
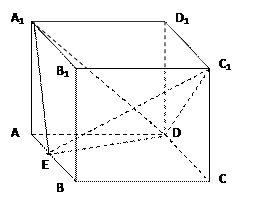
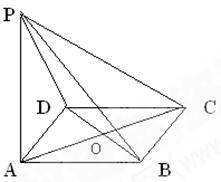
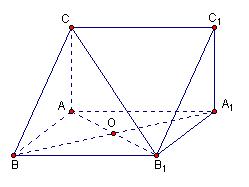
(本小题满分14分)如图,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
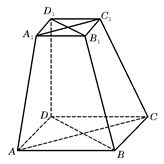
(Ⅰ)求证:A1C1与AC共面,B1D1与BD共面;
(Ⅱ)求证:平面A1ACC1⊥平面B1BDD1;
(Ⅲ)求二面角A-BB1-C的大小(用反三角函数值表示).

(Ⅰ)求证:A1C1与AC共面,B1D1与BD共面;
(Ⅱ)求证:平面A1ACC1⊥平面B1BDD1;
(Ⅲ)求二面角A-BB1-C的大小(用反三角函数值表示).
(Ⅰ)证明见解析
(Ⅱ)证明见解析
(Ⅲ)二面角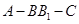 的大小为
的大小为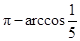
(Ⅱ)证明见解析
(Ⅲ)二面角
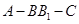 的大小为
的大小为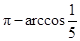
解法1(向量法):
以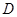 为原点,以
为原点,以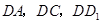 所在直线分别为
所在直线分别为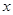 轴,
轴,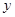 轴,
轴,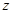 轴建立空间直角坐标系
轴建立空间直角坐标系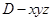 如图,
如图,
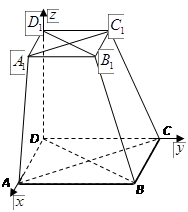
则有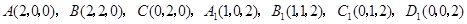 .
.
(Ⅰ)证明:
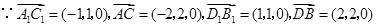 .
.
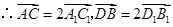 .
.
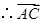 与
与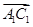 平行,
平行,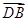 与
与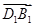 平行,
平行,
于是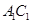 与
与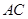 共面,
共面,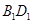 与
与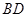 共面.
共面.
(Ⅱ)证明: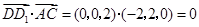 ,
,
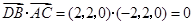 ,
,
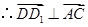 ,
,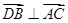 .
.
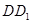 与
与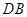 是平面
是平面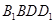 内的两条相交直线.
内的两条相交直线.
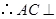 平面
平面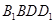 .
.
又平面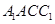 过
过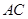 .
.
 平面
平面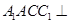 平面
平面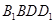 .
.
(Ⅲ)解: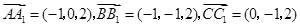 .
.
设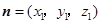 为平面
为平面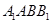 的法向量,
的法向量,
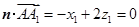 ,
,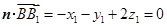 .
.
于是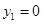 ,取
,取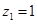 ,则
,则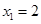 ,
,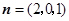 .
.
设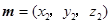 为平面
为平面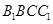 的法向量,
的法向量,
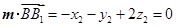 ,
,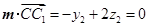 .
.
于是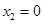 ,取
,取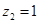 ,则
,则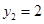 ,
,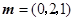 .
.
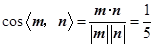 .
.
 二面角
二面角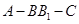 的大小为
的大小为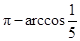 .
.
解法2(综合法):
(Ⅰ)证明: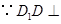 平面
平面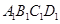 ,
,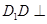 平面
平面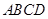 .
.
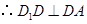 ,
,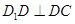 ,平面
,平面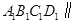 平面
平面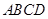 .
.
于是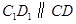 ,
,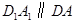 .
.
设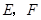 分别为
分别为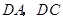 的中点,连结
的中点,连结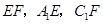 ,
,
有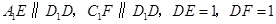 .
.
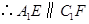 ,
,
于是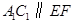 .
.
由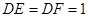 ,得
,得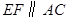 ,
,
故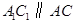 ,
,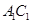 与
与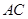 共面.
共面.
过点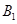 作
作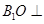 平面
平面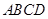 于点
于点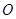 ,
,
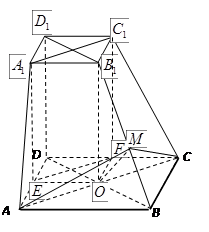
则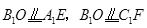 ,连结
,连结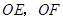 ,
,
于是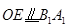 ,
,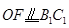 ,
,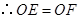 .
.
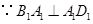 ,
,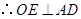 .
.
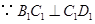 ,
,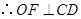 .
.
所以点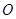 在
在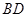 上,故
上,故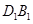 与
与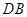 共面.
共面.
(Ⅱ)证明: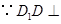 平面
平面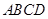 ,
,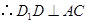 ,
,
又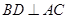 (正方形的对角线互相垂直),
(正方形的对角线互相垂直),
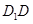 与
与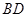 是平面
是平面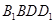 内的两条相交直线,
内的两条相交直线,
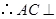 平面
平面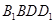 .
.
又平面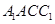 过
过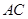 ,
, 平面
平面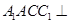 平面
平面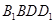 .
.
(Ⅲ)解: 直线
直线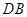 是直线
是直线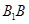 在平面
在平面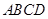 上的射影,
上的射影,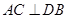 ,
,
根据三垂线定理,有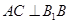 .
.
过点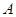 在平面
在平面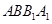 内作
内作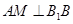 于
于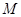 ,连结
,连结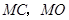 ,
,
则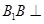 平面
平面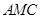 ,
,
于是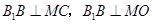 ,
,
所以,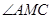 是二面角
是二面角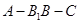 的一个平面角.
的一个平面角.
根据勾股定理,有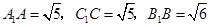 .
.
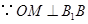 ,有
,有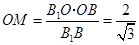 ,
,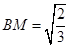 ,
,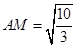 ,
,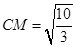 .
.
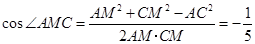 ,
,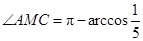 ,
,
二面角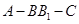 的大小为
的大小为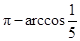 .
.
以
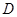 为原点,以
为原点,以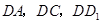 所在直线分别为
所在直线分别为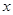 轴,
轴,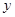 轴,
轴,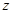 轴建立空间直角坐标系
轴建立空间直角坐标系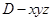 如图,
如图,
则有
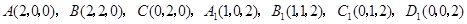 .
.(Ⅰ)证明:
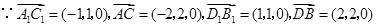 .
.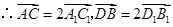 .
.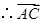 与
与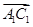 平行,
平行,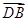 与
与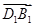 平行,
平行,于是
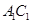 与
与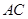 共面,
共面,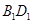 与
与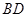 共面.
共面.(Ⅱ)证明:
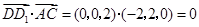 ,
,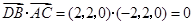 ,
,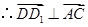 ,
,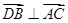 .
.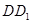 与
与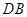 是平面
是平面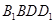 内的两条相交直线.
内的两条相交直线.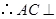 平面
平面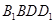 .
.又平面
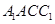 过
过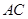 .
. 平面
平面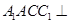 平面
平面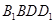 .
.(Ⅲ)解:
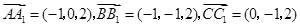 .
.设
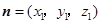 为平面
为平面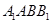 的法向量,
的法向量,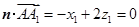 ,
,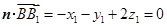 .
.于是
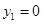 ,取
,取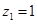 ,则
,则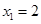 ,
,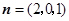 .
.设
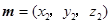 为平面
为平面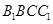 的法向量,
的法向量,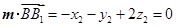 ,
,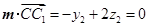 .
.于是
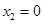 ,取
,取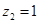 ,则
,则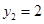 ,
,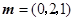 .
.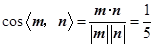 .
. 二面角
二面角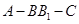 的大小为
的大小为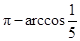 .
.解法2(综合法):
(Ⅰ)证明:
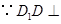 平面
平面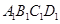 ,
,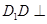 平面
平面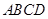 .
.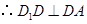 ,
,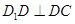 ,平面
,平面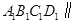 平面
平面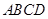 .
.于是
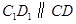 ,
,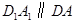 .
.设
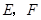 分别为
分别为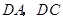 的中点,连结
的中点,连结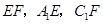 ,
,有
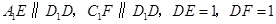 .
.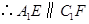 ,
,于是
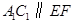 .
.由
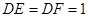 ,得
,得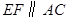 ,
,故
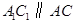 ,
,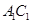 与
与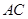 共面.
共面.过点
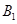 作
作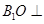 平面
平面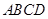 于点
于点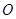 ,
,
则
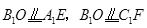 ,连结
,连结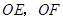 ,
,于是
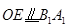 ,
,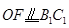 ,
,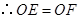 .
.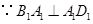 ,
,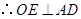 .
.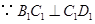 ,
,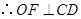 .
.所以点
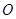 在
在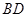 上,故
上,故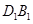 与
与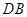 共面.
共面.(Ⅱ)证明:
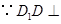 平面
平面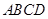 ,
,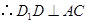 ,
,又
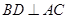 (正方形的对角线互相垂直),
(正方形的对角线互相垂直),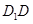 与
与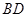 是平面
是平面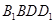 内的两条相交直线,
内的两条相交直线,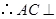 平面
平面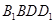 .
.又平面
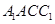 过
过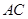 ,
, 平面
平面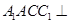 平面
平面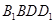 .
.(Ⅲ)解:
 直线
直线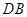 是直线
是直线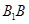 在平面
在平面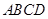 上的射影,
上的射影,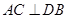 ,
,根据三垂线定理,有
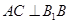 .
.过点
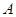 在平面
在平面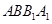 内作
内作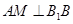 于
于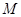 ,连结
,连结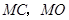 ,
,则
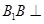 平面
平面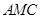 ,
,于是
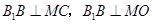 ,
,所以,
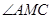 是二面角
是二面角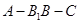 的一个平面角.
的一个平面角.根据勾股定理,有
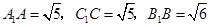 .
.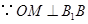 ,有
,有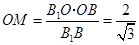 ,
,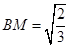 ,
,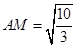 ,
,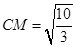 .
.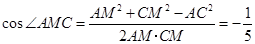 ,
,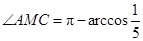 ,
,二面角
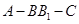 的大小为
的大小为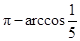 .
.
练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
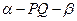 ,
,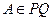 ,
,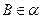 ,
,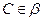 ,
,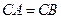 ,
,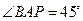 ,直线
,直线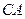 和平面
和平面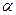 所成的角为
所成的角为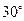 .
.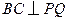 ;
;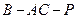 的大小.
的大小.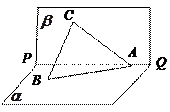
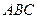 中,
中,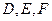 分别为各边的中点,
分别为各边的中点,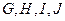 分别为
分别为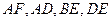 的中点,将
的中点,将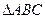 沿
沿 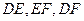 折成三棱锥后,
折成三棱锥后,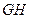 与
与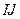 所成的角的度数为____。
所成的角的度数为____。 
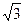 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.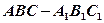 ,已知
,已知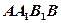 是正方形且边长为
是正方形且边长为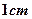 ,
,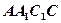 为矩形,且平面
为矩形,且平面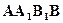
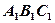 ⊥平面
⊥平面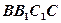 ;
;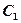 到平面
到平面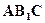 的距离。
的距离。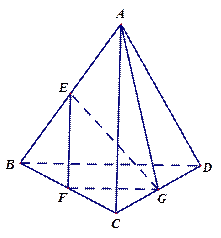
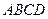 中,
中,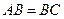 ,
,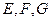 分别是
分别是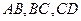 的中点,且
的中点,且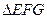 为正三角形,
为正三角形,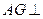 平面
平面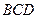 .
.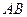 与平面
与平面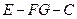 的平面角的余弦值.
的平面角的余弦值.