题目内容
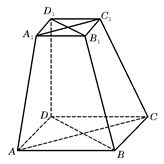
(本小题满分14分)如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
(I)求证:平面A1ED⊥平面ABB1A1;
(II)求二面角A1-ED-C1的余弦值;
(III)求点C1到平面A1ED的距离。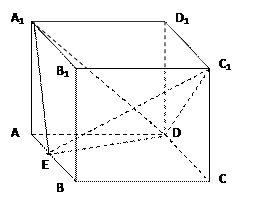
(I)求证:平面A1ED⊥平面ABB1A1;
(II)求二面角A1-ED-C1的余弦值;
(III)求点C1到平面A1ED的距离。

(I)同解析,(II)二面角A1-ED-C1的余弦值为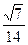 (III)点C1到平面A1ED的距离为
(III)点C1到平面A1ED的距离为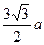 (
(
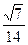 (III)点C1到平面A1ED的距离为
(III)点C1到平面A1ED的距离为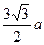 (
(解:(I)证明:连结BD,在菱形ABCD中,∠BAD=600,∴△ABD为正三角形,
∵E为AB的中点,∴ED⊥AB (1分)
在直六面体ABCD-A1B1C1D1中:
平面ABB1A1⊥平面ABCD且交于AB,∵ED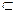 面ABCD∴ED⊥面ABB1A1(3分)
面ABCD∴ED⊥面ABB1A1(3分)
∴平面A1ED⊥平面ABB1A1(4分)
(II)解:由(I)知:ED⊥面ABB1A1∵A1E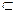 面ABB1A1∴A1E⊥ED
面ABB1A1∴A1E⊥ED
又在直平行六面体ABCD-A1B1C1D1中:AA1⊥面ABCD,
由三垂线定理的逆定理知:AE⊥ED,∴∠A1EA=600(5分)
取BB1的中点F,连EF.AB1,则EF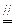
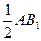 ,在直平行六面体ABCD-A1B1C1D1中:AB1
,在直平行六面体ABCD-A1B1C1D1中:AB1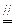 DC1∴EF
DC1∴EF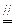
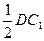 ∴E.F.C1、D四点共面(6分)
∴E.F.C1、D四点共面(6分)
∵ED⊥面ABB1A1且EF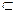 面ABB1A1
面ABB1A1
∴EF⊥ED∴∠A1EF为二面角A1-ED-C1的平面角(7分)
在Rt△A1AE中: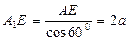 ,
,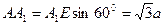
在Rt△EBF中: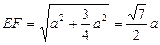 ,
,
在Rt△A1B1F中: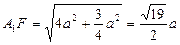
∴在Rt△A1EF中: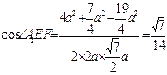 ,∴二面角A1-ED-C1的余弦值为
,∴二面角A1-ED-C1的余弦值为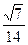 (9分)
(9分)
(III)过F作FG⊥A1E交A1E于G点∵平面A1ED⊥面ABB1A1
且平面A1ED∩面ABB1A1=A1E∴FG⊥平面A1ED,
即:FG是点F到平面A1ED的距离(11分)
在Rt△EGF中: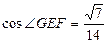 ∴
∴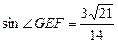
∴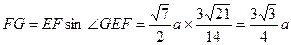 (13分)
(13分)
∵EF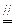
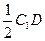 且E.D∈面A1ED∴点C1到平面A1ED的距离为
且E.D∈面A1ED∴点C1到平面A1ED的距离为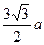 (14分)
(14分)
∵E为AB的中点,∴ED⊥AB (1分)
在直六面体ABCD-A1B1C1D1中:
平面ABB1A1⊥平面ABCD且交于AB,∵ED
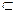 面ABCD∴ED⊥面ABB1A1(3分)
面ABCD∴ED⊥面ABB1A1(3分)∴平面A1ED⊥平面ABB1A1(4分)
(II)解:由(I)知:ED⊥面ABB1A1∵A1E
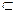 面ABB1A1∴A1E⊥ED
面ABB1A1∴A1E⊥ED又在直平行六面体ABCD-A1B1C1D1中:AA1⊥面ABCD,
由三垂线定理的逆定理知:AE⊥ED,∴∠A1EA=600(5分)
取BB1的中点F,连EF.AB1,则EF
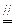
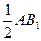 ,在直平行六面体ABCD-A1B1C1D1中:AB1
,在直平行六面体ABCD-A1B1C1D1中:AB1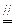 DC1∴EF
DC1∴EF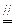
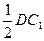 ∴E.F.C1、D四点共面(6分)
∴E.F.C1、D四点共面(6分)∵ED⊥面ABB1A1且EF
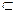 面ABB1A1
面ABB1A1∴EF⊥ED∴∠A1EF为二面角A1-ED-C1的平面角(7分)
在Rt△A1AE中:
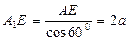 ,
,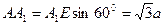
在Rt△EBF中:
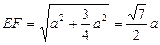 ,
,在Rt△A1B1F中:
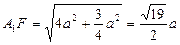
∴在Rt△A1EF中:
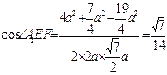 ,∴二面角A1-ED-C1的余弦值为
,∴二面角A1-ED-C1的余弦值为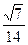 (9分)
(9分)(III)过F作FG⊥A1E交A1E于G点∵平面A1ED⊥面ABB1A1
且平面A1ED∩面ABB1A1=A1E∴FG⊥平面A1ED,
即:FG是点F到平面A1ED的距离(11分)
在Rt△EGF中:
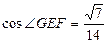 ∴
∴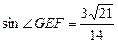
∴
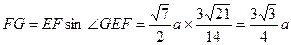 (13分)
(13分)∵EF
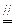
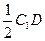 且E.D∈面A1ED∴点C1到平面A1ED的距离为
且E.D∈面A1ED∴点C1到平面A1ED的距离为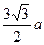 (14分)
(14分)
练习册系列答案
相关题目
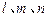 及平面
及平面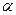 ,下列命题中的假命题是 ( )
,下列命题中的假命题是 ( )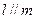 ,
,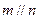 ,则
,则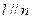
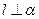 ,
,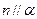 ,则
,则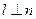
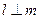 ,
,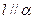 ,
,

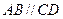 ,
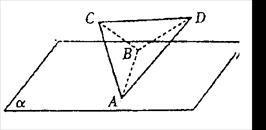
,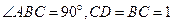 ,AB=2,E为AB的中点,将
,AB=2,E为AB的中点,将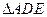 沿DE翻折至
沿DE翻折至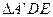 ,使二面角A
,使二面角A
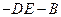 为直二面角。
为直二面角。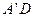 、
、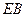 的中点,求证:
的中点,求证: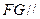 平面
平面 ;
; 度数的余弦值
度数的余弦值
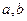 是两条不同的直线,
是两条不同的直线,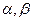 是两个不重合的平面,则下列命题中正确的是 ( )
是两个不重合的平面,则下列命题中正确的是 ( )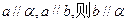
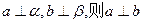
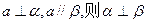
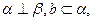 则
则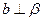
 D的棱长为1,棱AB//平面
D的棱长为1,棱AB//平面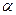 ,则正四面体上的所有点在平面
,则正四面体上的所有点在平面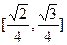
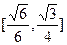
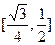
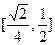
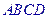 各边
各边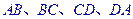 上分别取
上分别取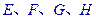 四点,如果与
四点,如果与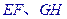 能相交于点
能相交于点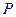 ,那么( )
,那么( ) 上
上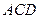 外
外 外
外 、
、 ,两个不同的平面
,两个不同的平面 则下列命题中正确的是 ( )
则下列命题中正确的是 ( ) ,则
,则
 则
则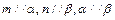 则
则
 则
则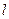 及两个平面
及两个平面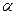 、
、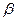 ,下列命题正确的是 ( )
,下列命题正确的是 ( )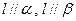 ,则
,则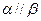
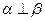
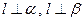 , 则
, 则