题目内容
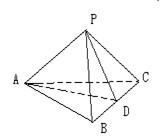
(本题满分10分)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,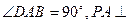 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=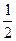 AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
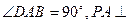 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=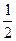 AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。 (2)
(2)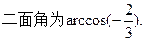
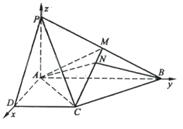
:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),
M(0,1,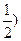 .
.
(Ⅰ)证明:因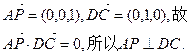 由题设知AD⊥DC,且AP与AD是平面PAD内的两
由题设知AD⊥DC,且AP与AD是平面PAD内的两
条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD. 3分
(Ⅱ)解:因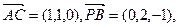
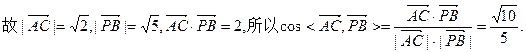 6分
6分
(Ⅲ)解:在MC上取一点N(x,y,z),则存在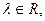 使
使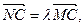
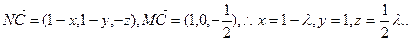
要使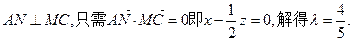 8分
8分

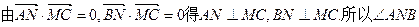 为所求二面角的平面角.
为所求二面角的平面角.
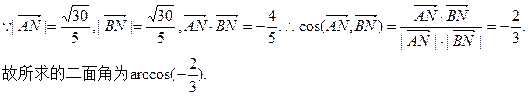
10分
点评:本题考查空间向量的运用,用空间向量研究线面垂直、求线面所成角、面面所成角,属于中档与较难题
M(0,1,
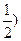 .
.
|
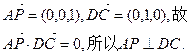 由题设知AD⊥DC,且AP与AD是平面PAD内的两
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD. 3分
(Ⅱ)解:因
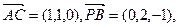
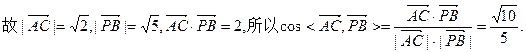 6分
6分(Ⅲ)解:在MC上取一点N(x,y,z),则存在
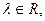 使
使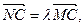
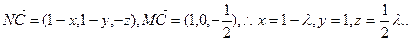
要使
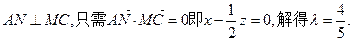 8分
8分
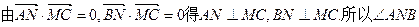 为所求二面角的平面角.
为所求二面角的平面角.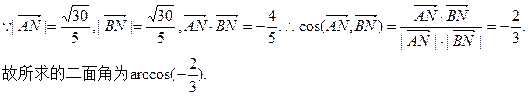
10分
点评:本题考查空间向量的运用,用空间向量研究线面垂直、求线面所成角、面面所成角,属于中档与较难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC
平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC