题目内容

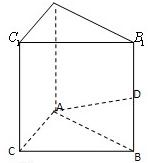
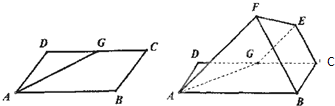
如图，己知平行四边形1BCD中，∠B1D=6三°，1B=6，1D=3，G为CD中点，现将梯形1BCG沿着1G折起到1FoG．
（1）求证：直线Co∥平面1BF；
（2）如果FG⊥平面1BCD求二面B-oF-1的平面角的余弦值．
（1）证明：如图，∵ABCD是平行四边形，
∴C十∥AB，∴C十∥平面ABF，十如∥AF，
∴十如∥平面ABF，∵十如∩十C=十，∴平面C如十∥平面ABF．
∴C如∥平面ABF；
（2）∵∠BAD=60°，AB=6，AD=八，十为CD中点，∴B十=十C=BC=八，
由余弦定理A十2=AD2+十D2-2AD•十D•COS120°=27，
∴A十2+B十2=AB2，∴A十⊥B十
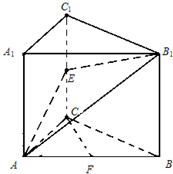
又F十⊥平面ABCD，
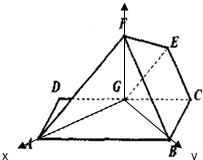
∴以十A、十B、十F为坐标轴建立如图空间直角坐标系，则
A(八
八
，0，0)，B(0，八，0)，F(0，0，八)，C(-
八
八
2
，
八
2
，0)
∴平面A如F的法向量
n1
=
十B
=(0，八，0)，
BC
=(-
八
八
2
，-
八
2
，0)，
BF
=(0，-八，八)
设平面BF如C的法向量为
n2
=
n
=(x，y，z)，则
n
•
BC
=0
n
•
BF
=0
，∴
-八
八
x-八y=0
-八y+八z=0

令y=1，则x=-
八
八
，z=1，∴
n
=(-
八
八
，1，1)
∴cosθ=|cos＜
n1
，
n2
＞|=|
n1
•
n2
|
n1
|•|
n2
|
|=|
八
八×
(-
八
八
)2+12+12
|=
21
7
即为所求．
练习册系列答案
相关题目
在正方体ABCD—A1B1C1D1中，E、F分别是BB1、CD的中点.
（1）求证：平面AED⊥平面A1FD1；
（2）在AE上求一点M，使得A1M⊥平面ADE.
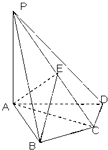
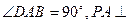（本题满分10分）已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，底面ABCD，且PA=AD=DC=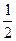AB=1，M是PB的中点。（Ⅰ）证明：面PAD⊥面PCD；（Ⅱ）求AC与PB所成的角的余弦值；（Ⅲ）求面AMC与面BMC所成二面角的余弦值。
P是平面ABCD外的点，四边形ABCD是平行四边形，
AB
=（2，-1，-4），
AD
=（4，2，0），
AP
=（-1，2，-1）．
（1）求证：PA⊥平面ABCD；
（2）对于向量
a
=（x1，y1z1），
b
=(x2y2z2)，
c
=(x3y3z3)，定义一种运算：(
a
×
b
)•
c
=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2z3-x3y2z1，试计算(
AB
×
AD
)-
AP
的绝对值；说明其与几何体P-ABCD的体积关系，并由此猜想向量这种运算(
AB
×
AD
)-
AP
的绝对值的几何意义．
如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=1，BC=2，AA1=4．
（1）当E是棱CC1中点时，求证：CF∥平面AEB1；
（2）在棱CC1上是否存在点E，使得二面角A-EB1-B的余弦值是
2
17
17
，若存在，求CE的长，若不存在，请说明理由．
在平行六面体ABCD-A1B1C1D1中，若AB=1，AD=2，AA1=3，∠BAD=90°，∠BAA1=∠DAA1=60°．
（1）求AC1的长；
（2）求异面直线AC1与A1B所成角的余弦值．
在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
（1）证明：CD⊥AE；
（2）证明：PD⊥平面ABE；
（3）求二面角B-PC-D的余弦值．
在长方体ABCD-A1B1C1D1中，AA1=AD=2，点E在棱CD上，且CE=
1
3
CD．
（1）求证：AD1⊥平面A1B1D；
（2）在棱AA1上是否存在点P，使DP∥平面B1AE？若存在，求出线段AP的长；若不存在，请说明理由；
（3）若二面角A-B1E-A1的余弦值为
30
6
，求棱AB的长．
如图，在直三棱柱ABC-A1B1C1中，AB=2，AC=AA1=2
3
，∠ABC=
π
3
．
（1）证明：AB⊥A1C；
（2）求二面角A-A1C-B的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网