题目内容
16.通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的性别与看营养列联表:| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)先求出每个个体被抽到的概率,再用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数.
(2)从这5名女生中随机选取两名,共有10个等可能的基本事件,其中,事件A“选到看与不看营养说明的女生各一名”包含了6个的基本事件,由此求得所求的概率.
(3)根据性别与看营养说明列联表,求出K2的观测值k的值为7.486>6.635,再根据P(K2≥6.635)=0.01,该校高中学生“性别与在购买食物时看营养说明”有关.
解答 解:(1)根据分层抽样可得:样本中看营养说明的女生有$\frac{5}{50}×30$=3名,
样本中不看营养说明的女生有$\frac{5}{50}×20$=2 名.…(2分)
(2)记样本中看营养说明的3名女生为a1、a2、a3,不看营养说明的2名女生为b1、b2,
从这5名女生中随机选取两名,共有10个等可能的基本事件为:(a1、a2);( a1、a3); (a1、b1);
( a1、b2);(a2、a3);(a2、b1);(a2、b2);(a3、b1);(a3、b2);(b1、b2).…(5分)
其中,事件A“选到看与不看营养说明的女生各一名”包含了6个的基本事件:(a1、b1);( a1、b2);
(a2、b1);(a2、b2);(a3、b1);(a3、b2).…(7分)
所以所求的概率为P(A)=$\frac{6}{10}$=$\frac{3}{5}$.…(9分)
(3)性别与看营养说明列联表 单位:名
| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
根据题中的列联表得K2=$\frac{110×(50×20-30×10)^{2}}{80×30×60×50}$≈7.486>6.635,…(11分)
由P(K2≥6.635)=0.01,
有99%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关.…(12分)
点评 本题主要考考查读图表、抽样方法、随机事件的概率、独立性检验等基础知识,考查运用概率统计知识解决简单实际问题的能力,数据处理能力和应用意识,属于基础题.

练习册系列答案
相关题目
6.E、F分别是边长为1的正方形ABCD边BC、CD的中点,沿线AF,AE,EF折起来,则所围成的三棱锥的体积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
7.C${\;}_{3}^{0}$+C${\;}_{4}^{1}$+C${\;}_{5}^{2}$+C${\;}_{6}^{3}$+…+C${\;}_{20}^{17}$的值为( )
| A. | C${\;}_{21}^{3}$ | B. | C${\;}_{20}^{3}$ | C. | C${\;}_{20}^{4}$ | D. | C${\;}_{21}^{4}$ |
1.从一批含有13只正品,2只次品的产品中,不放回地任取3件,则取得次品数为1件的概率是( )
| A. | $\frac{32}{35}$ | B. | $\frac{12}{35}$ | C. | $\frac{3}{35}$ | D. | $\frac{2}{35}$ |
8.AB是圆O内的一条弦,圆O半径是5,且圆心到AB的距离为3,则弦AB的长度为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
5.已知全集U={a,b,c,d,e},集合A={b,c},∁UB={c,d},则(∁UA)∩B等于( )
| A. | {a,e} | B. | {b,c,d} | C. | {a,c,e} | D. | {c} |
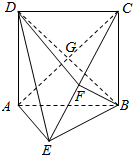 如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G
如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G