题目内容
4.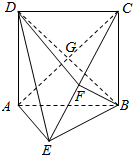 如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G
如图,矩形ABCD中,BC⊥平面ABE,且BC=4,AE=EB,F为CE的中点,且BF⊥平面ACE,B∩AC=G (1)求证:AE∥平面BFD;
(2)求证:AE⊥平面BCE;
(3)求三棱锥E-ADC的体积.
分析 (1)连接GF,由三角形的中位线可得到GF∥AE,再由线面平行的判定定理得证;
(2)证明AE⊥平面BCE,利用线面垂直的判定定理,只需证明AE⊥BC,BF⊥AE即可;
(3)证明OE⊥平面ADC,再用三棱锥的体积公式求解.
解答  (1)证明:连结 GF,矩形ABCD中,BD∩AC=G
(1)证明:连结 GF,矩形ABCD中,BD∩AC=G
∴G为AC中点,又F为CE的中点,
∴GF∥AE.…(2分)
∵AE?平面BFD,GF?平面BFD,∴AE∥平面BFD.…(3分)
(2)证明:∵BC⊥平面ABE,AE?平面ABE,∴BC⊥AE.
又∵BF⊥平面ACE,AE?平面AEC,∴BF⊥AE,…(5分)
∵BC∩BF=BH,且BC,BF?平面BCE,
∴AE⊥平面BCE …(6分)
(3)解:取AB中点O,连结OE,
∵AE=EB,∴OE⊥AB
∵BC⊥平面ABE,∴OE⊥BC,
又∵AB∩BC=B,AB、BC?平面ABCD,
∴OE⊥平面ADC …(8分)
∵BF⊥平面ACE,CE?平面ACE,∴BF⊥CE,
又F为CE的中点,∴BC=BE=4,…(10分)
由(2)知AE⊥平面BCE,又BE?平面BCE,∴AE⊥EB.
∴△AEB为等腰直角三角形,∴$AB=\sqrt{A{E^2}+B{E^2}}=4\sqrt{2}$…(12分)
∴$OE=\frac{1}{2}AB=2\sqrt{2}$,
故三棱锥E-ADC的体积为:${V_{E-ADC}}=\frac{1}{3}{S_{△ADC}}.OE=\frac{1}{3}×\frac{1}{2}×4×4\sqrt{2}×2\sqrt{2}=\frac{32}{3}$…(14分)
点评 本题主要考查线线,线面关系的转化,考查了线面平行,垂直的判定定理以及三棱锥体积的求法,属中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.将点(2,3)变成点(3,2)的伸缩变换是( )
| A. | $\left\{\begin{array}{l}x'=\frac{2}{3}x\\ y'=\frac{3}{2}y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=\frac{3}{2}x\\ y'=\frac{2}{3}y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=y\\ y'=x\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=x+1\\ y'=y-1\end{array}\right.$ |
16.通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的性别与看营养列联表:
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为5的样本,问样本中看与不看营养说明的女生各有多少名?
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8.
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8. 如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.
如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.