题目内容
6.已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且∠C=$\frac{2π}{3}$,c=$\sqrt{3}$.(1)若sinA=$\frac{1}{4}$,求cosB的值;
(2)求△ABC周长的取值范围.
分析 (1)运用同角的平方关系,结合诱导公式和两角和的余弦公式计算即可得到;
(2)由正弦定理可得a=2sinA,b=2sinB,再由两角和差的正弦公式,结合余弦函数的性质,计算即可得到所求范围.
解答 解:(1)若sinA=$\frac{1}{4}$,A为锐角,
则cosA=$\sqrt{1-\frac{1}{16}}$=$\frac{\sqrt{15}}{4}$,
cosB=-cos(A+C)=-cos(A+$\frac{2π}{3}$)
=-(-$\frac{1}{2}$cosA-$\frac{\sqrt{3}}{2}$sinA)
=$\frac{1}{2}×\frac{\sqrt{15}}{4}$+$\frac{\sqrt{3}}{2}×\frac{1}{4}$=$\frac{\sqrt{15}+\sqrt{3}}{8}$;
(2)由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{\sqrt{3}}{sin\frac{2π}{3}}$=2,
即有a=2sinA,b=2sinB,
设A=$\frac{π}{6}$-α,B=$\frac{π}{6}$+α,-$\frac{π}{6}$<α<$\frac{π}{6}$,
即有a+b=2[sin($\frac{π}{6}$-α)+sin($\frac{π}{6}$+α)]
=4sin$\frac{π}{6}$cosα=2cosα,
由-$\frac{π}{6}$<α<$\frac{π}{6}$,则cosα∈($\frac{\sqrt{3}}{2}$,1],
即有周长a+b+c的范围是(2$\sqrt{3}$,$\sqrt{3}$+2].
点评 本题考查正弦定理的运用,两角和差的正弦、余弦公式和余弦函数的性质的运用,考查运算能力,属于中档题.

| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
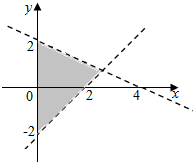
| A. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4>0\\ x≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4>0\\ x≥0\end{array}\right.$ |
 如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.
如图,$|\overrightarrow{AO}|=1$,P是以AB为直径的半圆弧上的动点,以CP为一边作正△CPD,则$|\overrightarrow{OD}|$的最大值是4.