E.F分别是边长为1的正方形ABCD边BC.CD的中点.沿线AF.AE.EF折起来.则所围成的三棱锥的体积为( )A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{1}{12}$D．$\frac{1}{24}$ 题目和参考答案——青夏教育精英家教网—

题目内容

6．E、F分别是边长为1的正方形ABCD边BC、CD的中点，沿线AF，AE，EF折起来，则所围成的三棱锥的体积为（　　）

A．

$\frac{1}{3}$

B．

$\frac{1}{6}$

C．

$\frac{1}{12}$

D．

$\frac{1}{24}$

分析由题意图形折叠为三棱锥，直接求出三棱柱的体积即可．

解答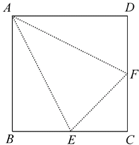解：由题意图形折叠为三棱锥，底面为直角△EFC，高为1，
所以三棱柱的体积：$\frac{1}{3}$×$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{24}$，
故选：D．

点评本题是基础题，考查几何体的体积的求法，注意折叠问题的处理方法，考查计算能力．

练习册系列答案

17．i为虚数单位，则（1-i）²的虚部为（　　）

14．若关于x的方程sin²x+sinx-1+m=0有解，则实数m的取值范围为[-1，$\frac{5}{4}$]．

1．已知角α的顶点在坐标原点上，角α的始边与x轴的正半轴重合，并且角α的终边在射线y=-2x（x≤0）上，则cosα=$-\frac{{\sqrt{5}}}{5}$．

11．（Ⅰ）计算（$\frac{1-i}{1+i}$）²
（Ⅱ）已知复数z满足：|z|=1+3i-z，求$\frac{（1+i）^{2}（3+4i）^{2}}{2z}$的值．

18．已知点P在曲线y=x³-x+$\frac{2}{3}$上移动，设点P处切线的倾斜角为α，则α的取值范围是（　　）

A．

[0，$\frac{π}{2}$]

B．

[0，$\frac{π}{2}$]∪（-$\frac{π}{2}$，0）

C．

[$\frac{3π}{4}$，π]

D．

[0，$\frac{π}{2}$）∪[$\frac{3π}{4}$，π）

15．已知函数f（x）=e^x-ax-1．
（1）当a=e时，求f（x）的单调区间；
（2）若对任意x≥0，都有f（x）≥0，求实数a的取值范围．

16．通过随机询问某校110名高中学生在购买食物时是否看营养说明，得到如下的性别与看营养列联表：

	男	女	总计
看营养说明	50	30	80
不看营养说明	10	20	30
总计	60	50	110

（1）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为5的样本，问样本中看与不看营养说明的女生各有多少名？
（2）从（1）中的5名女生样本中随机选取两名作深度访谈，求选到看与不看营养说明的女生各一名的概率；
（3）根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？
K²=$\frac{m（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$

p（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

试题分类