题目内容
1.从一批含有13只正品,2只次品的产品中,不放回地任取3件,则取得次品数为1件的概率是( )| A. | $\frac{32}{35}$ | B. | $\frac{12}{35}$ | C. | $\frac{3}{35}$ | D. | $\frac{2}{35}$ |
分析 有题意知本题是一个等可能事件的概率,试验发生包含的事件是从15件产品中抽取3件,共有C153=455,满足条件的事件是取得一件次品,共有C132C21=156,由此能求出取得一件次品的概率.
解答 解:试验发生包含的事件是从15件产品中抽取3件,共有C153=455,满足条件的事件是取得一件次品,共有C132C21=156,
故取得次品数为1件的概率是$\frac{156}{455}$=$\frac{12}{35}$,
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
16.通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的性别与看营养列联表:
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为5的样本,问样本中看与不看营养说明的女生各有多少名?
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女生样本中随机选取两名作深度访谈,求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
K2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.设变量x,y满足$\left\{\begin{array}{l}{x-y≥-1}\\{x+y≥1}\\{3x-y≤3}\end{array}\right.$,则w=4x+y的最大值为( )
| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
11.如图所示,表示阴影部分的二元一次不等式组是( )
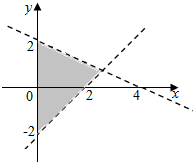

| A. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4>0\\ x≥0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y-2<0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4<0\\ x≥0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y-2>0\\ x+2y-4>0\\ x≥0\end{array}\right.$ |
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8.
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8.