题目内容
2.已知椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$的右焦点为F.短轴的一个端点为M,直线l:3x-4y=0,若点M到直线l的距离不小于$\frac{4}{5}$,则椭圆E的离心率的取值范围是(0,$\frac{\sqrt{3}}{2}$].分析 求得椭圆的短轴的一个端点,运用点到直线的距离公式解不等式可得1≤b<2,运用离心率公式,以及不等式的性质,即可得到所求范围.
解答 解:椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$的短轴的一个端点为M(0,b),
点M到直线l的距离不小于$\frac{4}{5}$,即为$\frac{4b}{\sqrt{9+16}}$≥$\frac{4}{5}$,
即有1≤b<2,又a=2,c=$\sqrt{4-{b}^{2}}$,
则e=$\frac{c}{a}$=$\frac{\sqrt{4-{b}^{2}}}{2}$∈(0,$\frac{\sqrt{3}}{2}$].
故答案为:(0,$\frac{{\sqrt{3}}}{2}$].
点评 本题考查椭圆的离心率的范围,考查点到直线的距离公式的运用,以及不等式的解法和性质,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10.下列函数中,值域为(0,+∞)的是( )
| A. | y=-5x | B. | $y={(\frac{1}{3})^{1-x}}$ | ||
| C. | y=x2-2x+3,x∈(-∞,2] | D. | $y=\frac{1}{x+1},x∈[0,+∞)$ |
17.以双曲线$\frac{x^2}{4}-{y^2}=1$的中心为顶点,右焦点为焦点的抛物线方程是( )
| A. | y2=4x | B. | ${y^2}=4\sqrt{5}x$ | C. | ${y^2}=8\sqrt{5}x$ | D. | ${y^2}=\sqrt{5}x$ |
7.在△ABC中,角A、B、C所对的边分别是a、b、c,满足acosA+bcosB=ccosC,则△ABC为( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
14.设△ABC的内角A,B,C所对边的长分别为a,b,c,若a:b:c=1:2:$\sqrt{7}$,则角C=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
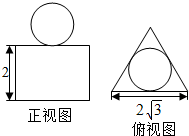 如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.
如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.