Question

13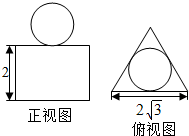．如图一个几何体的正视图和俯视图如图所示，其中俯视图为边长为2$\sqrt{3}$的正三角形，且圆与三角形内切，则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$．

Answer 1

分析 几何体是三棱柱与球的组合体，判断三棱柱的高及底面三角形的边长，计算球的半径，进而计算棱柱和球的体积，相加可得答案．

解答 解：由三视图知：几何体是三棱柱与球的组合体，
其中三棱柱的高为2，底面三角形的边长为2$\sqrt{3}$，故底面面积S=$\frac{\sqrt{3}}{4}×（2\sqrt{3}）^{2}$=3$\sqrt{3}$，
故圆柱的体积V=2×3$\sqrt{3}$=6$\sqrt{3}$，
根据俯视图是一个圆内切于一个正三角形，球的半径R=$\frac{1}{3}$×2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=1，故球的体积为：$\frac{4π}{3}$
故组合体的体积为：$6\sqrt{3}+\frac{4π}{3}$，
故答案为：$6\sqrt{3}+\frac{4π}{3}$

点评 本题考查了由正视图与俯视图求体积，判断数据所对应的几何量及求得相关几何量的数据是解题的关键