题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{sinπx,x∈[0,2]}\\{\frac{1}{2}f(x-2),x∈(2,+∞)}\end{array}\right.$,g(x)=ln(x-1),则函数h(x)=f(x)-g(x)的零点个数( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由分段函数的表达式,求出x>2的解析式,画出y=f(x)的图象和y=ln(x-1)的图象,由图象观察交点个数,即为函数零点个数.
解答  解:令y=0则f(x)=ln(x-1)
解:令y=0则f(x)=ln(x-1)
当2<x≤4时,0<x-2≤2,
f(x)=$\frac{1}{2}$sinπ(x-2);
当4<x≤6时,0<x-4≤2,
f(x)=$\frac{1}{4}$sinπ(x-4);
…
画出y=f(x)的图象和y=ln(x-1)的图象,
由图象可知交点个数为3,
即函数y=f(x)-ln(x-1)的零点个数为3,
故选:B.
点评 本题考查分段函数的图象和应用,考查函数的零点个数转化为函数图象交点个数,考查数形结合的能力,是一道中档题.

练习册系列答案
相关题目
17.函数f(x)=log3(4x-1)的定义域为( )
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2},+∞$) | C. | ($\frac{1}{4},\frac{1}{2}$] | D. | ($\frac{1}{4},+∞$) |
4.已知f(x)=3x+4,若|f(x)-1|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
| A. | $a>\frac{b}{3}$ | B. | $b<\frac{a}{3}$ | C. | $a≤\frac{b}{3}$ | D. | $b≥\frac{a}{3}$ |
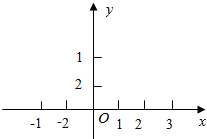 已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,(-1≤x≤1)}\\{x-1,(x≥1)}\end{array}\right.$.