题目内容
【题目】选修4-5:不等式选讲
已知函数f(x)=|x+2|﹣2|x﹣1|.
(Ⅰ)求不等式f(x)≥﹣2的解集M;
(Ⅱ)对任意x∈[a,+∞],都有f(x)≤x﹣a成立,求实数a的取值范围.
【答案】(Ⅰ)解:∵函数f(x)=|x+2|﹣2|x﹣1|,∴不等式f(x)≥﹣2即 ![]() ①,或
①,或 ![]() ②,或
②,或 ![]() ③.
③.
解①求得x∈,解②求得﹣ ![]() ≤x<1,解③求得1≤x≤6,
≤x<1,解③求得1≤x≤6,
综上,不等式的解集为M={x|﹣ ![]() ≤x≤6}.
≤x≤6}.
(Ⅱ)对任意x∈[a,+∞],都有f(x)≤x﹣a成立,函数f(x)= 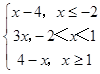 的图象如图所示:
的图象如图所示:
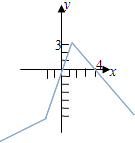
令y=x﹣a,则此直线斜率为1,﹣a表示直线的纵截距,故函数f(x)的图象在直线y=x﹣a的下方或在直线上.
当直线过(1,3)点时,﹣a=2,即a=﹣2;
∴当﹣a≥2,即a≤﹣2时,条件成立;
当﹣a<2,即a>﹣2时,令﹣x+4=x﹣a,得x=2+ ![]() ,
,
∴a≥2+ ![]() ,即a≥4时,条件成立,
,即a≥4时,条件成立,
综上a≤﹣2或a≥4.
【解析】(Ⅰ)通过对x≤﹣2,﹣2<x<1与x≥1三类讨论,去掉绝对值符号,解相应的一次不等式,最后取其并集即可;(Ⅱ)在坐标系中,作出f(x)= 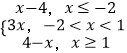 的图象,对任意x∈[a,+∞),都有f(x)≤x﹣a成立,分﹣a≥2与﹣a<2讨论,即可求得实数a的取值范围.
的图象,对任意x∈[a,+∞),都有f(x)≤x﹣a成立,分﹣a≥2与﹣a<2讨论,即可求得实数a的取值范围.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据(xi , yi)(i=1,2,…,6),如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知 ![]() =80.
=80.
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程 ![]() ;可供选择的数据:
;可供选择的数据: ![]() ,
, ![]()
(Ⅲ)用 ![]() 表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi , yi)对应的残差的绝对值
表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi , yi)对应的残差的绝对值 ![]() 时,则将销售数据(xi , yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
时,则将销售数据(xi , yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
(参考公式:线性回归方程中 ![]() ,
, ![]() 的最小二乘估计分别为
的最小二乘估计分别为  ,
, ![]() )
)