题目内容
【题目】平面直角坐标系xOy中,已知椭圆 ![]() 的左焦点为F,离心率为
的左焦点为F,离心率为 ![]() ,过点F且垂直于长轴的弦长为
,过点F且垂直于长轴的弦长为 ![]() .
.
(I)求椭圆C的标准方程;
(Ⅱ)设点A,B分别是椭圆的左、右顶点,若过点P(﹣2,0)的直线与椭圆相交于不同两点M,N.
(i)求证:∠AFM=∠BFN;
(ii)求△MNF面积的最大值.
【答案】解:(I)由题意可得 ![]() ,
,
令x=﹣c,可得y=±b ![]() =±
=± ![]() ,
,
即有 ![]() ,又a2﹣b2=c2,
,又a2﹣b2=c2,
所以 ![]() .
.
所以椭圆的标准方程为 ![]() ;
;
(II)方法一、(i)当AB的斜率为0时,显然∠AFM=∠BFN=0,满足题意;
当AB的斜率不为0时,设A(x1,y1),B(x2,y2),AB方程为x=my﹣2,
代入椭圆方程,整理得(m2+2)y2﹣4my+2=0,
则△=16m2﹣8(m2+2)=8m2﹣16>0,所以m2>2.
 ,
,
可得 ![]() =
= 
= 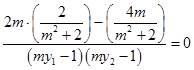 .
.
则kMF+kNF=0,即∠AFM=∠BFN;
(ii) 
当且仅当 ![]() ,即m2=6.(此时适合△>0的条件)取得等号.
,即m2=6.(此时适合△>0的条件)取得等号.
则三角形MNF面积的最大值是 ![]() .
.
方法二(i)由题知,直线AB的斜率存在,设直线AB的方程为:y=k(x+2),
设A(x1,y1),B(x2,y2),
联立  ,整理得(1+2k2)x2+8k2x+8k2﹣2=0,
,整理得(1+2k2)x2+8k2x+8k2﹣2=0,
则△=64k4﹣4(1+2k2)(8k2﹣2)=8﹣16k2>0,所以 ![]() .
.
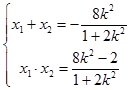 ,
,
可得 ![]()
= 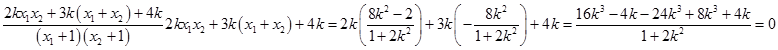
∴kMF+kNF=0,即∠AFM=∠BFN;
(ii)  ,
,
点F(﹣1,0)到直线MN的距离为 ![]() ,
,
即有 ![]() =
=  =
=  .
.
令t=1+2k2,则t∈[1,2),u(t)=  ,
,
当且仅当 ![]() ,即
,即 ![]() (此时适合△>0的条件)时,
(此时适合△>0的条件)时, ![]() ,
,
即 ![]() ,则三角形MNF面积的最大值是
,则三角形MNF面积的最大值是 ![]() .
.
【解析】(1)运用椭圆的离心率公式和过焦点垂直于对称轴的弦长,结合a,b,c的关系解得a,b,可得椭圆的方程;(II)方法一、(i)讨论直线AB的斜率为0和不为0,设A(x1,y1),B(x2,y2),AB方程为x=my﹣2,代入椭圆方程,运用韦达定理和判别式大于0,运用直线的斜率公式求斜率之和,即可得证;(ii)求得△MNF的面积 ![]() ,化简整理,运用基本不等式可得最大值.方法二、(i)由题知,直线AB的斜率存在,设直线AB的方程为:y=k(x+2),设A(x1,y1),B(x2,y2),联立椭圆方程,消去y,可得x的方程,运用韦达定理和判别式大于0,再由直线的斜率公式,求得即可得证;(ii)求得弦长|MN|,点F到直线的距离d,运用三角形的面积公式,化简整理,运用换元法和基本不等式,即可得到所求最大值.
,化简整理,运用基本不等式可得最大值.方法二、(i)由题知,直线AB的斜率存在,设直线AB的方程为:y=k(x+2),设A(x1,y1),B(x2,y2),联立椭圆方程,消去y,可得x的方程,运用韦达定理和判别式大于0,再由直线的斜率公式,求得即可得证;(ii)求得弦长|MN|,点F到直线的距离d,运用三角形的面积公式,化简整理,运用换元法和基本不等式,即可得到所求最大值.

【题目】已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示: 
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.