题目内容
【题目】如图,已知中心在原点,焦点在x轴上的椭圆的一个焦点为( ![]() ,0),(1,
,0),(1, ![]() )是椭圆上的一个点.
)是椭圆上的一个点. 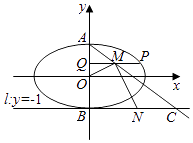
(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为A,B,P(x0 , y0)(x0≠0)是椭圆上异于A,B的任意一点,PQ⊥y轴,Q为垂足,M为线段PQ中点,直线AM交直线l:y=﹣1于点C,N为线段BC的中点,如果△MON的面积为 ![]() ,求y0的值.
,求y0的值.
【答案】
(1)解:设椭圆方程为 ![]() ,由题意,得
,由题意,得 ![]() .
.
因为a2﹣c2=b2,所以b2=a2﹣3.
又 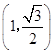 是椭圆上的一个点,所以
是椭圆上的一个点,所以  ,解得a2=4或
,解得a2=4或 ![]() (舍去),
(舍去),
从而椭圆的标准方程为 ![]()
(2)解:因为P(x0,y0),x0≠0,则Q(0,y0),且 ![]() .
.
因为M为线段PQ中点,所以 ![]() .
.
又A(0,1),所以直线AM的方程为 ![]() .
.
因为x0≠0,∴y0≠1,令y=﹣1,得 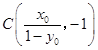 .
.
又B(0,﹣1),N为线段BC的中点,有  .
.
所以 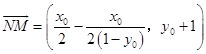 .
.
因此, 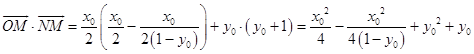
= 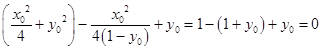 .从而OM⊥MN.
.从而OM⊥MN.
因为 ![]() ,
, 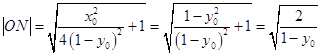 ,
,
所以在Rt△MON中, ![]() ,因此
,因此  .
.
从而有 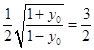 ,解得
,解得 ![]()
【解析】(1)确定 ![]() ,利用
,利用 ![]() 是椭圆上的一个点,代入求出a,即可求椭圆的标准方程;(2)求出M,N的坐标,利用平面向量的数量积判断OM⊥MN,利用△MON的面积为
是椭圆上的一个点,代入求出a,即可求椭圆的标准方程;(2)求出M,N的坐标,利用平面向量的数量积判断OM⊥MN,利用△MON的面积为 ![]() ,建立方程,即可求y0的值.
,建立方程,即可求y0的值.

练习册系列答案
相关题目
【题目】已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示: 
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.