题目内容
【题目】已知椭圆 ![]() 的右焦点
的右焦点 ![]() ,且经过点
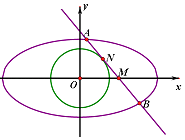
,且经过点 ![]() ,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方) 
(1)求椭圆C的方程;
(2)若|AM|=2|MB|,且直线l与圆 ![]() 相切于点N,求|MN|的长.
相切于点N,求|MN|的长.
【答案】
(1)解:由题意知: 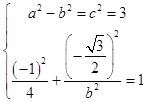 ,
,
a2=3+b2>3,解得:a2=4,b2=1,
故椭圆C的方程为 ![]() ;
;
(2)解:设M(m,0),直线l:x=ty+m,A(x1,y1),B(x2,y2),
由|AM|=2|MB|,有y1=﹣2y2,
由 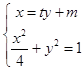 ,得(t2+4)y2+2my+m2﹣4=0,
,得(t2+4)y2+2my+m2﹣4=0,
由韦达定理得: ![]() ,
,
由 ![]() ,
,
得 ![]() ,即
,即 ![]() ,
,
化简得(m2﹣4)(t2+4)=﹣8t2m2,①
原点O到直线的距离 ![]() ,
,
又直线l与圆 ![]() 相切,
相切,
∴ 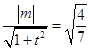 ,即
,即 ![]() ,②
,②
联立①②得:21m4﹣16m2﹣16=0,即(3m2﹣4)(7m2+4)=0,
解得 ![]() ,此时
,此时 ![]() ,满足△>0,得
,满足△>0,得 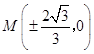 ,
,
在Rt△OMN中,可得 ![]() ,
,
∴|MN|的长为 ![]() .
.
【解析】(1)由题意列关于a,b的方程组,求解方程组可得a,b的值,则椭圆方程可求;(2)设出M,A,B的坐标及直线l的方程x=ty+m,与椭圆方程联立,化为关于y的一元二次方程,由|AM|=2|MB|,有y1=﹣2y2,再结合根与系数的关系可得m与t的关系,由直线与圆相切可得m与t的另一关系式,联立求得m,t的值,可得M的坐标,则|MN|的长可求.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示: 
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.