题目内容
已知非零向量a,b,c满足a+b+c=0,向量a与b的夹角为60°,且|a|=|b|=1,则向量a与c的夹角为( ).
| A.30° | B.60° | C.120° | D.150° |
D
因为a+b+c=0,所以c=-(a+b).所以|c|2=(a+b)2=a2+b2+2a·b=2+2cos 60°=3.所以|c|= .
.
又c·a=-(a+b)·a=-a2-a·b=-1-cos 60°=- ,设向量c与a的夹角为θ,则cos θ=
,设向量c与a的夹角为θ,则cos θ= =
= =-
=- .又0°≤θ≤180°,所以θ=150°.
.又0°≤θ≤180°,所以θ=150°.
 .
.又c·a=-(a+b)·a=-a2-a·b=-1-cos 60°=-
 ,设向量c与a的夹角为θ,则cos θ=
,设向量c与a的夹角为θ,则cos θ= =
= =-
=- .又0°≤θ≤180°,所以θ=150°.
.又0°≤θ≤180°,所以θ=150°.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +
+ -
- =0;
=0; +
+ )=0;
)=0;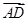 =
=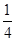 (
( 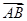 +
+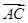 ),
),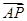 =
=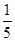
 ,则
,则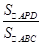 =________.
=________. ,
, ,且
,且 ,则 ( )
,则 ( )



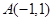 ,点
,点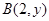 ,向量
,向量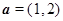 ,若
,若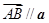 ,则实数
,则实数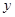 的值为( )
的值为( ) +
+ +
+ =
= ,则△PAB的面积与△ABC的面积比为( )
,则△PAB的面积与△ABC的面积比为( ) +
+ +
+ =λ
=λ ,则λ= .
,则λ= . ,
, ,若
,若 ∥
∥ ,则
,则 等于( ).
等于( ).


 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )


