题目内容
下列命题中是真命题的是( )
①对任意两向量a,b,均有:|a|-|b|<|a|+|b|;
②对任意两向量a,b,a-b与b-a是相反向量;
③在△ABC中, +
+ -
- =0;
=0;
④在四边形ABCD中,( +
+ )-(
)-( +
+ )=0;
)=0;
⑤在△ABC中, -
- =
=  .
.
①对任意两向量a,b,均有:|a|-|b|<|a|+|b|;
②对任意两向量a,b,a-b与b-a是相反向量;
③在△ABC中,
 +
+ -
- =0;
=0;④在四边形ABCD中,(
 +
+ )-(
)-( +
+ )=0;
)=0;⑤在△ABC中,
 -
- =
=  .
.| A.①②③ | B.②④⑤ |
| C.②③④ | D.②③ |
D
①假命题.∵当b=0时,|a|-|b|=|a|+|b|,∴该命题不成立.
②真命题.∵(a-b)+(b-a)=a+(-b)+b+(-a)=a+(-a)+b+(-b)=(a-a)+(b-b)=0,
∴a-b与b-a是相反向量.
③真命题.∵ +
+ -
- =
= -
- =0,
=0,
∴命题成立.
④假命题.∵ +
+ =
= ,
, +
+ =
= ,
,
∴( +
+ )-(
)-( +
+ )
)
= -
- =
= +
+ ≠0,
≠0,
∴该命题不成立.
⑤假命题.∵ -
- =
= +
+ =
= ≠
≠ ,
,
∴该命题不成立.
②真命题.∵(a-b)+(b-a)=a+(-b)+b+(-a)=a+(-a)+b+(-b)=(a-a)+(b-b)=0,
∴a-b与b-a是相反向量.
③真命题.∵
 +
+ -
- =
= -
- =0,
=0,∴命题成立.
④假命题.∵
 +
+ =
= ,
, +
+ =
= ,
,∴(
 +
+ )-(
)-( +
+ )
)=
 -
- =
= +
+ ≠0,
≠0,∴该命题不成立.
⑤假命题.∵
 -
- =
= +
+ =
= ≠
≠ ,
,∴该命题不成立.

练习册系列答案
相关题目
 ,则|b|= .
,则|b|= . ,
,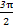 ).
). |=|
|=| |,求角α的值.
|,求角α的值.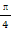 )的值.
)的值. =α
=α +β
+β ,其中α,β∈R且α+β=1,则点C的轨迹方程为( )
,其中α,β∈R且α+β=1,则点C的轨迹方程为( )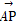 =
=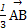 +t
+t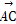 ,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )
,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )



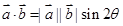 ,(其中
,(其中 为
为 、
、 的夹角),已知△ABC中,
的夹角),已知△ABC中,
 ,则此三角形一定是( )
,则此三角形一定是( )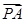 +
+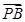 +
+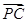 =
=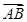 ,则△PBC与△ABC的面积之比是________.
,则△PBC与△ABC的面积之比是________. 等于( )
等于( )


