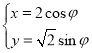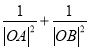题目内容
【题目】已知函数f(x)![]() (cosθ+1)cos2x+cosθ(cosx+1),有下述四个结论:①f(x)是偶函数;②f(x)在(
(cosθ+1)cos2x+cosθ(cosx+1),有下述四个结论:①f(x)是偶函数;②f(x)在(![]() ,
,![]() )上单调递减;③当θ∈[
)上单调递减;③当θ∈[![]() ,
,![]() ]时,有|f(x)|
]时,有|f(x)|![]() ;④当θ∈[
;④当θ∈[![]() ,
,![]() ]时,有|f'(x)|
]时,有|f'(x)|![]() ;其中所有真命题的编号是( )
;其中所有真命题的编号是( )
A.①③B.②④C.①③④D.①④
【答案】D
【解析】
对①直接进行奇偶性的判断即可,对②③④可用换元法,转化成二次函数的图像与性质进行判断即可.
①函数的定义域为R,
∵f(﹣x)=(cosθ+1)cos2(﹣x)+cosθ[cos(﹣x)+1]=(cosθ+1)cos2x+cosθ(cosx+1)=f(x),
∴f(x)是偶函数,即①正确;
②f(x)=2(cosθ+1)cos2x+cosθcosx﹣1,
设t=cosx,则f(t)=2(cosθ+1)t2+tcosθ﹣1,
∵2(cosθ+1)![]() 0,∴二次函数的开口向上,
0,∴二次函数的开口向上,
函数的对称轴为t![]() ,且t的正负与cosθ的取值有关,
,且t的正负与cosθ的取值有关,
∴f(x)在(![]() ,
,![]() )上不一定单调递减,即②错误;
)上不一定单调递减,即②错误;
③当θ∈[![]() ,
,![]() ]时,cosθ∈[
]时,cosθ∈[![]() ,
,![]() ],
],
f(x)=2(cosθ+1)cos2x+cosθcosx﹣1
设t=cosx,则t∈![]() ,
,
则f(t)=2(cosθ+1)t2+tcosθ﹣1,
∵2(cosθ+1)![]() 0,∴二次函数的开口向上,
0,∴二次函数的开口向上,
函数的对称轴为t![]() ,
,
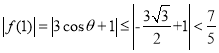 ,
,
![]() ,
,
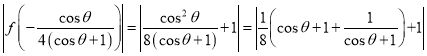 ,
,
当![]()
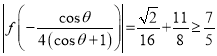 , 故③错误.
, 故③错误.
④当θ∈[![]() ,
,![]() ]时,cosθ∈[
]时,cosθ∈[![]() ,
,![]() ]
]
有![]()
![]() ,故④成立.
,故④成立.
故选:D.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.