题目内容
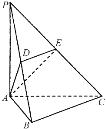
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 平面
平面![]() ,
,![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(1)若![]() ,求直线
,求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)若平面![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先取![]() 的中点
的中点![]() ,连接
,连接![]() ,以
,以![]() 为坐标原点,过
为坐标原点,过![]() 且与
且与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,分别求出
轴,建立空间直角坐标系,分别求出![]() ,
,![]() 的坐标,再代入公式计算即可.
的坐标,再代入公式计算即可.
(2)首先设![]() ,分别计算平面
,分别计算平面![]() 和平面
和平面![]() 的法向量,根据平面
的法向量,根据平面![]() 平面
平面![]() ,法向量的数量积等于
,法向量的数量积等于![]() 即可得到
即可得到![]() 的长.
的长.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
以![]() 为坐标原点,过
为坐标原点,过![]() 且与
且与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
![]() 为
为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
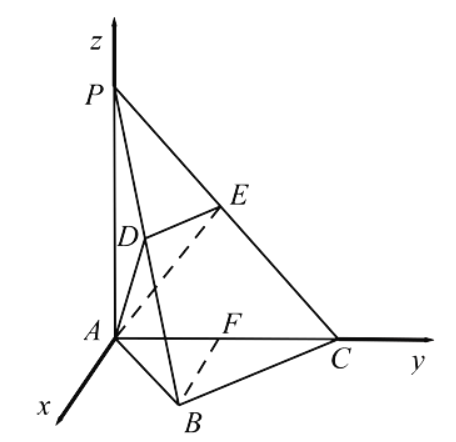
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
设直线![]() ,
,![]() 所成角为
所成角为![]() ,
,
则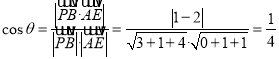 .
.
所以直线![]() ,
,![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(2)设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则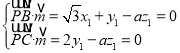 ,令
,令![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则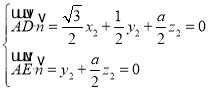 ,令
,令![]() ,
,![]() .
.
因为面![]() 平面
平面![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
所以![]() .
.

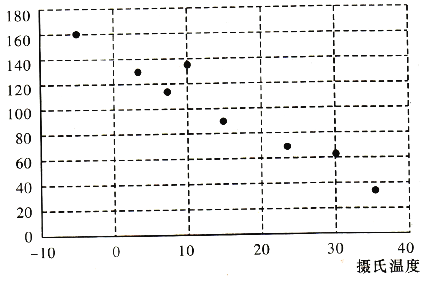
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表:
摄氏温度 |
|
|
|
|
|
|
|
|
热饮杯数 |
|
|
|
|
|
|
|
|
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里。因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少。统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(i)中求出的线性回归方程
.对于(i)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]()
![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
(参考公式)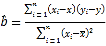 ,
,![]() ,
,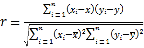
(参考数据)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.