ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Τϊ≥ΒΤΖ≈ΤΈΣΝΥΝΥΫβΩΆΜßΕ‘”ΎΤδΤλœ¬ΒΡΈε÷÷–ΆΚ≈Τϊ≥ΒΒΡ¬ζ“β«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ“Μ–©ΩΆΜßΫχ––ΜΊΖΟΘ§Βς≤ιΫαΙϊ»γœ¬±μΘΚ
Τϊ≥Β–ΆΚ≈ | I | II | III | IV | V |
ΜΊΖΟΩΆΜßΘ®»Υ ΐΘ© | 250 | 100 | 200 | 700 | 350 |
¬ζ“β¬ | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
¬ζ“β¬ «÷ΗΘΚΡ≥÷÷–ΆΚ≈Τϊ≥ΒΒΡΜΊΖΟΩΆΜß÷–Θ§¬ζ“β»Υ ΐ”κΉή»Υ ΐΒΡ±»÷Β.
ΦΌ…ηΩΆΜß «Ζώ¬ζ“βΜΞœύΕάΝΔΘ§«“ΟΩ÷÷–ΆΚ≈Τϊ≥ΒΩΆΜßΕ‘”Ύ¥Υ–ΆΚ≈Τϊ≥Β¬ζ“βΒΡΗ≈¬ ”κ±μΗώ÷–ΗΟ–ΆΚ≈Τϊ≥ΒΒΡ¬ζ“β¬ œύΒ».
(1)¥”Υυ”–ΒΡΜΊΖΟΩΆΜß÷–ΥφΜζ≥ι»Γ1»ΥΘ§«σ’βΗωΩΆΜ߬ζ“βΒΡΗ≈¬ ΘΜ
(2)¥”I–ΆΚ≈ΚΆV–ΆΚ≈Τϊ≥ΒΒΡΥυ”–ΩΆΜß÷–ΗςΥφΜζ≥ι»Γ1»ΥΘ§…ηΤδ÷–¬ζ“βΒΡ»Υ ΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘΜ
(3)”Ο ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜ߬ζ“βΘ§ ΓΑ
Γ±Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜ߬ζ“βΘ§ ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ±, ΓΑ
Γ±, ΓΑ![]() Γ± Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜß≤Μ¬ζ“β.–¥≥ωΖΫ≤ν
Γ± Ζ÷±π±μ ΨI, II, III, IV, V–ΆΚ≈Τϊ≥Β»ΟΩΆΜß≤Μ¬ζ“β.–¥≥ωΖΫ≤ν![]() ΒΡ¥σ–ΓΙΊœΒ.
ΒΡ¥σ–ΓΙΊœΒ.
ΓΨ¥πΑΗΓΩ(1) ![]() (2)ΦϊΫβΈωΘΜ(3)
(2)ΦϊΫβΈωΘΜ(3)![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©«σ≥ω―υ±Ψ÷–ΒΡΜΊΖΟΩΆΜßΒΡΉή ΐΚΆ¬ζ“βΒΡΩΆΜß»Υ ΐΘ§Φ¥Ω…«σ≥ωΗ≈¬ ΘΜ
Θ®2Θ©”…Χβ«σ≥ω¬ζ“βΒΡ»Υ ΐΈΣ![]() ΒΡΖ÷≤ΦΝ–Θ§ΦΧΕχ«σ≥ωΤΎΆϊ;
ΒΡΖ÷≤ΦΝ–Θ§ΦΧΕχ«σ≥ωΤΎΆϊ;
Θ®3Θ©ΗυΨίΙΪ Ϋ÷±Ϋ”ΒΟ≥ωΫαΙϊΘ§»ΜΚσΉς±»Ϋœ.
Θ®1Θ©”…Χβ“β÷ΣΘ§―υ±Ψ÷–ΒΡΜΊΖΟΩΆΜßΒΡΉή ΐ «![]() Θ§
Θ§
¬ζ“βΒΡΩΆΜß»Υ ΐ![]() Θ§
Θ§
Ι Υυ«σΗ≈¬ ΈΣ![]() Θ°
Θ°
Θ®2Θ©![]() .
.
…η ¬Φΰ![]() ΈΣΓΑ¥”I–ΆΚ≈Τϊ≥ΒΥυ”–ΩΆΜß÷–ΥφΜζ≥ι»ΓΒΡ»Υ¬ζ“βΓ±Θ§
ΈΣΓΑ¥”I–ΆΚ≈Τϊ≥ΒΥυ”–ΩΆΜß÷–ΥφΜζ≥ι»ΓΒΡ»Υ¬ζ“βΓ±Θ§
¬Φΰ![]() ΈΣΓΑ¥”V–ΆΚ≈Τϊ≥ΒΥυ”–ΩΆΜß÷–ΥφΜζ≥ι»ΓΒΡ»Υ¬ζ“βΓ±Θ§«“
ΈΣΓΑ¥”V–ΆΚ≈Τϊ≥ΒΥυ”–ΩΆΜß÷–ΥφΜζ≥ι»ΓΒΡ»Υ¬ζ“βΓ±Θ§«“![]() ΓΔ
ΓΔ![]() ΈΣΕάΝΔ ¬Φΰ.
ΈΣΕάΝΔ ¬Φΰ.
ΗυΨίΧβ“βΘ§![]() ΙάΦΤΈΣ0.5Θ§
ΙάΦΤΈΣ0.5Θ§![]() ΙάΦΤΈΣ0.2 .
ΙάΦΤΈΣ0.2 .
‘ρ![]() ;
;
![]()
![]() ;
;
![]() .
.
![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
|
|
|
|
|
|
|
|
![]() ΒΡΤΎΆϊ
ΒΡΤΎΆϊ![]()
Θ®3Θ©”…ΧβΘ§I–ΆΚ≈ΒΡΤΫΨυ ΐΈΣ0.5,Υυ“‘![]() =
=![]()
Ά§άμ![]() =
=![]()
Ά§άμ![]() =0.24ΘΜ
=0.24ΘΜ![]() =0.21ΘΜ
=0.21ΘΜ![]() =0.16
=0.16
Υυ“‘![]() Θ°
Θ°

ΓΨΧβΡΩΓΩΡ≥–ΘΗΏ»ΐΘ®1Θ©Αύ‘Ύ“Μ¥Έ”οΈΡ≤β ‘Ϋα χΚσΘ§ΖΔœ÷Ά§―ßΟ«‘Ύ±≥Υ–ΡΎ»ίΖΫΟφ ßΖ÷ΫœΈΣ―œ÷Ί.ΈΣΝΥΧα…ΐ±≥Υ––ßΙϊΘ§Αύ÷ς»Έ≥Ϊ“ι¥σΦ“‘Ύ‘γïäΕΝ ±Φδ’ΨΤπά¥¥σ…υΥ–ΕΝΘ§ΈΣΝΥΫβΆ§―ßΟ«Ε‘’ΨΤπά¥¥σ…υΥ–ΕΝΒΡΧ§Ε»Θ§Ε‘»ΪΑύ50ΟϊΆ§―ßΫχ––Βς≤ιΘ§ΫΪΒς≤ιΫαΙϊΫχ––’ϊάμΚσ÷Τ≥…»γ±μΘΚ
ΩΦ ‘Ζ÷ ΐ |
|
|
|
|
|
|
ΤΒ ΐ | 5 | 10 | 15 | 5 | 10 | 5 |
‘ό≥…»Υ ΐ | 4 | 6 | 9 | 3 | 6 | 4 |
Θ®1Θ©”ϊ Ι≤β ‘”≈–ψ¬ ΈΣ![]() Θ§‘ρ”≈–ψΖ÷ ΐœΏ”ΠΕ®ΈΣΕύ…ΌΖ÷ΘΩ
Θ§‘ρ”≈–ψΖ÷ ΐœΏ”ΠΕ®ΈΣΕύ…ΌΖ÷ΘΩ
Θ®2Θ©“άΨίΒΎ1Έ ΒΡΫαΙϊΦΑ―υ±Ψ ΐΨί―–ΨΩ «Ζώ‘ό≥…’ΨΤπά¥¥σ…υΥ–ΕΝΒΡΧ§Ε»”κΩΦ ‘≥…Φ® «Ζώ”≈–ψΒΡΙΊœΒΘ§Ν–≥ω2ΓΝ2Ν–ΝΣ±μΘ§≤Δ≈–Εœ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣ‘ό≥…”κΖώΒΡΧ§Ε»”κ≥…Φ® «Ζώ”≈–ψ”–ΙΊœΒ.
ΒΡΑ―Έ’»œΈΣ‘ό≥…”κΖώΒΡΧ§Ε»”κ≥…Φ® «Ζώ”≈–ψ”–ΙΊœΒ.
≤ΈΩΦΙΪ ΫΦΑ ΐΨίΘΚ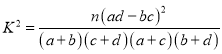 Θ§
Θ§![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
ΓΨΧβΡΩΓΩ”–“ΜΗωΆ§―ßΦ“ΩΣΝΥ“ΜΗω–Γ¬τ≤ΩΘ§ΥϊΈΣΝΥ―–ΨΩΤχΈ¬Ε‘»»“ϊ“ϊΝœœζ έΒΡ”ΑœλΘ§Ψ≠ΙΐΆ≥ΦΤΘ§ΒΟΒΫ“ΜΗω¬τ≥ωΒΡ»»“ϊ±≠ ΐ”κΒ±ΧλΤχΈ¬ΒΡ…ΔΒψΆΦΚΆΕ‘±»±μΘΚ
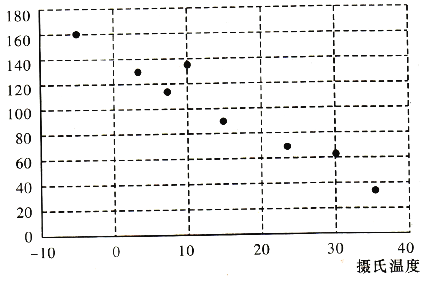
…ψ œΈ¬Ε» |
|
|
|
|
|
|
|
|
»»“ϊ±≠ ΐ |
|
|
|
|
|
|
|
|
Θ®1Θ©¥”…ΔΒψΆΦΩ…“‘ΖΔœ÷Θ§ΗςΒψ…Δ≤Φ‘Ύ¥”Ήσ…œΫ«ΒΫ”“œ¬Ϋ«ΒΡ«χ”ράοΓΘ“ρ¥ΥΘ§ΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐ÷°Φδ≥…ΗΚœύΙΊΘ§Φ¥ΤχΈ¬‘ΫΗΏΘ§Β±Χλ¬τ≥ω»ΞΒΡ»»“ϊ±≠ ΐ‘Ϋ…ΌΓΘΆ≥ΦΤ÷–≥Θ”ΟœύΙΊœΒ ΐ![]() ά¥ΚβΝΩΝΫΗω±δΝΩ÷°ΦδœΏ–‘ΙΊœΒΒΡ«Ω»θ.Ά≥ΦΤ―ß»œΈΣΘ§Ε‘”Ύ±δΝΩ
ά¥ΚβΝΩΝΫΗω±δΝΩ÷°ΦδœΏ–‘ΙΊœΒΒΡ«Ω»θ.Ά≥ΦΤ―ß»œΈΣΘ§Ε‘”Ύ±δΝΩ![]() ΓΔ
ΓΔ![]() Θ§»γΙϊ
Θ§»γΙϊ![]() Θ§Ρ«Ο¥ΗΚœύΙΊΚή«ΩΘΜ»γΙϊ
Θ§Ρ«Ο¥ΗΚœύΙΊΚή«ΩΘΜ»γΙϊ![]() Θ§Ρ«Ο¥’ΐœύΙΊΚή«ΩΘΜ»γΙϊ
Θ§Ρ«Ο¥’ΐœύΙΊΚή«ΩΘΜ»γΙϊ![]() Θ§Ρ«Ο¥œύΙΊ–‘“ΜΑψΘΜ»γΙϊ
Θ§Ρ«Ο¥œύΙΊ–‘“ΜΑψΘΜ»γΙϊ![]() Θ§Ρ«Ο¥œύΙΊ–‘Ϋœ»θΓΘ«κΗυΨί“―÷Σ ΐΨίΘ§≈–ΕœΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐœύΙΊ–‘ΒΡ«Ω»θ.
Θ§Ρ«Ο¥œύΙΊ–‘Ϋœ»θΓΘ«κΗυΨί“―÷Σ ΐΨίΘ§≈–ΕœΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐœύΙΊ–‘ΒΡ«Ω»θ.
Θ®2Θ©Θ®iΘ©«κΗυΨί“―÷Σ ΐΨί«σ≥ωΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®iiΘ©Φ«![]() ΈΣ≤Μ≥§Ιΐ
ΈΣ≤Μ≥§Ιΐ![]() ΒΡΉν¥σ’ϊ ΐΘ§»γ
ΒΡΉν¥σ’ϊ ΐΘ§»γ![]() Θ§
Θ§![]() .Ε‘”ΎΘ®iΘ©÷–«σ≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥Χ
.Ε‘”ΎΘ®iΘ©÷–«σ≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() Θ§ΫΪ
Θ§ΫΪ![]() ”ΈΣΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐΒΡΚ· ΐΙΊœΒ.“―÷ΣΤχΈ¬
”ΈΣΤχΈ¬”κΒ±Χλ»»“ϊœζ έ±≠ ΐΒΡΚ· ΐΙΊœΒ.“―÷ΣΤχΈ¬![]() ”κΒ±Χλ»»“ϊΟΩ±≠ΒΡœζ έάϊ»σ
”κΒ±Χλ»»“ϊΟΩ±≠ΒΡœζ έάϊ»σ![]() ΒΡΙΊœΒ «
ΒΡΙΊœΒ «![]()
![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ§«κΈ Β±ΤχΈ¬
Θ®ΒΞΈΜΘΚ‘ΣΘ©Θ§«κΈ Β±ΤχΈ¬![]() ΈΣΕύ…Ό ±Θ§Β±ΧλΒΡ»»“ϊœζ έάϊ»σΉήΕνΉν¥σΘΩ
ΈΣΕύ…Ό ±Θ§Β±ΧλΒΡ»»“ϊœζ έάϊ»σΉήΕνΉν¥σΘΩ
Θ®≤ΈΩΦΙΪ ΫΘ©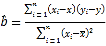 Θ§
Θ§![]() Θ§
Θ§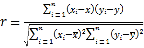
Θ®≤ΈΩΦ ΐΨίΘ©![]() Θ§
Θ§![]() Θ§
Θ§![]()
![]() .
.
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.