题目内容
【题目】如图,在直五棱柱,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
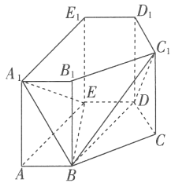
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先由题意可得![]() 且
且![]() ,从而有
,从而有![]() 平面
平面![]() ,即有
,即有![]() ,再结合
,再结合![]() 即可证明
即可证明![]() 平面
平面![]() ;
;
(2) 以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,然后写出相关点的坐标,求出相关平面的法向量,代入数量积求夹角公式即可.
,然后写出相关点的坐标,求出相关平面的法向量,代入数量积求夹角公式即可.
(1)证明:因为五棱柱![]() 为直五棱柱,
为直五棱柱,
所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.

(2)解:因为![]() ,所以
,所以![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,且
,且![]() 两两垂直.
两两垂直.
以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,
轴的正方向,
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则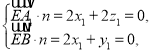
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则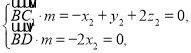
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
则 .
.

 阅读快车系列答案
阅读快车系列答案【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表:
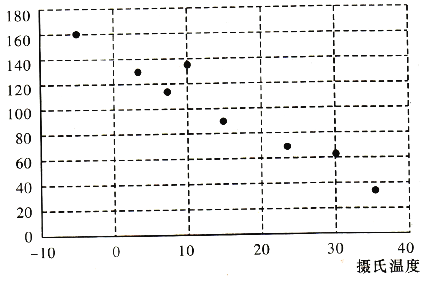
摄氏温度 |
|
|
|
|
|
|
|
|
热饮杯数 |
|
|
|
|
|
|
|
|
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里。因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少。统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(i)中求出的线性回归方程
.对于(i)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]()
![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
(参考公式)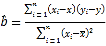 ,
,![]() ,
,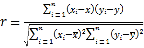
(参考数据)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中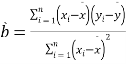
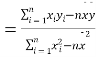 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)