题目内容
【题目】过抛物线![]() 上点
上点![]() 作三条斜率分别为
作三条斜率分别为![]() ,
,![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,与抛物线分别交于不同于
,与抛物线分别交于不同于![]() 的点
的点![]() .若
.若![]() ,
,![]() ,则以下结论正确的是( )
,则以下结论正确的是( )
A.直线![]() 过定点B.直线
过定点B.直线![]() 斜率一定
斜率一定
C.直线![]() 斜率一定D.直线
斜率一定D.直线![]() 斜率一定
斜率一定
【答案】B
【解析】
由题意,![]() ,
,![]() ,
,![]() 均不为0,设
均不为0,设![]() ,则
,则![]() ,同理可得
,同理可得![]()
![]() ,
,![]()
![]() ,由
,由![]() ,得
,得![]() ,再设出直线
,再设出直线![]() 的方程为
的方程为![]() ,利用韦达定理即可判断选项A、B,同理判断选项C、D.
,利用韦达定理即可判断选项A、B,同理判断选项C、D.
由题意,![]() ,
,![]() ,
,![]() 均不为0,设
均不为0,设![]() ,
,
则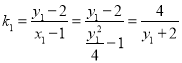 ,同理可得
,同理可得![]()
![]() ,
,
![]()
![]() ,由
,由![]() ,得
,得![]()
![]() ,即
,即![]() ,①
,①
设直线![]() 的方程为
的方程为![]() ,联立抛物线方程可得
,联立抛物线方程可得![]() ,
,
则![]() ,
,![]() 代入①式可得
代入①式可得![]() ,
,![]() ,
,
此时直线![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 斜率是定值,故B正确,A错误;
斜率是定值,故B正确,A错误;
由![]() ,得
,得![]()
![]() ,即
,即![]() ,②,同理设直线
,②,同理设直线
![]() 的方程为
的方程为![]() ,联立抛物线方程可得
,联立抛物线方程可得![]() ,
,
则![]() ,
,![]() 代入②式可得
代入②式可得![]() ,此时
,此时![]() 的方程为
的方程为
![]() ,恒过定点
,恒过定点![]() ,斜率不是定值,故C错误;
,斜率不是定值,故C错误;
由![]() ,
,![]() ,得
,得![]() ,即
,即![]()
![]() ,
,
即![]() ③,同理设直线
③,同理设直线![]() 的方程为
的方程为![]() ,联立抛物线方程可
,联立抛物线方程可
得![]() ,则
,则![]() ,
,![]() 代入③式可得
代入③式可得
![]() ,此时
,此时![]() 的方程为
的方程为![]() 恒过定点
恒过定点![]() ,斜率不为定值.
,斜率不为定值.
故D错误.
故选:B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目