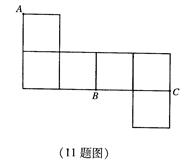
题目内容
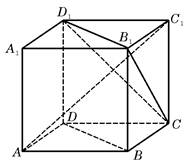
如图,ABCD-A1B1C1D1为正方体,则以下结论:
①BD∥平面CB1D1;
②AC1⊥BD;
③AC1⊥平面CB1D1
其中正确结论的个数是 ( )
①BD∥平面CB1D1;
②AC1⊥BD;
③AC1⊥平面CB1D1
其中正确结论的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |

D;
都正确,证明如下:
①因为BD∥B1D1,而且BD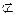 平面CB1D1,B1D1
平面CB1D1,B1D1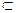 平面CB1D1;所以BD∥平面CB1D1;
平面CB1D1;所以BD∥平面CB1D1;
②由AC⊥BD,CC1⊥BD知BD⊥平面ACC1;所以BD⊥AC1;
③同②可证B1C⊥平面ABC1,所以B1C⊥AC1;又由AC1⊥BD、BD∥B1D1得AC1⊥B1D1;所以AC1⊥平面CB1D1..
①因为BD∥B1D1,而且BD
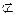 平面CB1D1,B1D1
平面CB1D1,B1D1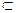 平面CB1D1;所以BD∥平面CB1D1;
平面CB1D1;所以BD∥平面CB1D1;②由AC⊥BD,CC1⊥BD知BD⊥平面ACC1;所以BD⊥AC1;
③同②可证B1C⊥平面ABC1,所以B1C⊥AC1;又由AC1⊥BD、BD∥B1D1得AC1⊥B1D1;所以AC1⊥平面CB1D1..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
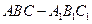 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是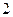 .
.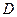 为侧棱
为侧棱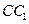 的中点,
的中点,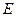 为底面一边
为底面一边 的中点.
的中点.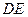 与
与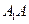 所成的角;
所成的角;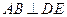 ;
;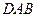 的距离.
的距离.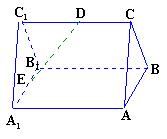
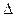 ABD和
ABD和 AC=
AC=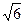 。
。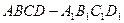 中,
中,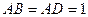 ,
,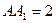 ,点
,点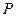 为
为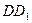 的中点。
的中点。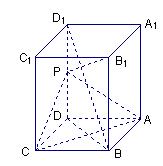
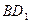 ∥平面
∥平面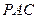 ;
;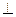 平面
平面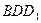 ;
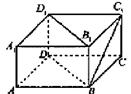
;
 平面
平面 =
= ,
, ,且
,且 ,二面角
,二面角 .
.  到平面
到平面 的大小为
的大小为 ,求
,求 的值.
的值.
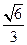
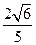
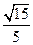
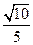
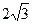 ,侧棱与底面所成的角为
,侧棱与底面所成的角为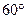 ,则该棱锥的体积为( )
,则该棱锥的体积为( ) ,直线
,直线 ,给出下列命题
,给出下列命题 ∥
∥ ;②
;② ∥m;③
∥m;③ ∥
∥ ;④
;④ ∥
∥ .
.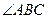 的度数为 .
的度数为 .