题目内容
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则BC1与平面BB1D1D所成角的正弦值为（ ）
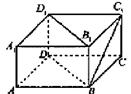
A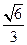． | B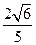． | C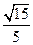． | D． |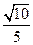
D
连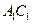
与
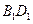交与O点，再连BO，则
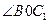为所成角，下面就是计算了。
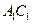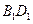与交与O点，再连BO，则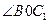为所成角，下面就是计算了。
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
新题型全程检测期末冲刺100分系列答案题目内容
| A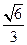． | B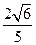． | C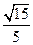． | D． |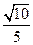
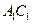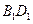与交与O点，再连BO，则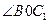为所成角，下面就是计算了。新题型全程检测期末冲刺100分系列答案
中，平面
侧面。
；
中，
底面
，
，
，
。
平面
；
的余弦值。
中，面
为矩形，
面
时，平面PBD⊥平面PAC；
时，求二面角
的取值范围。
中，
是
的中点，
，
．（Ⅰ）求证：
平面
；（Ⅱ）求异面直线
与
所成角的大小；
的大小．
与平面
,沿对角线AC把它折成直二面角B－AC－D后,BD=
,求AB、BC的长.
