题目内容
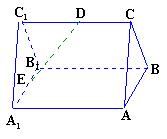
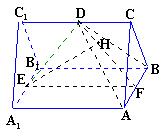
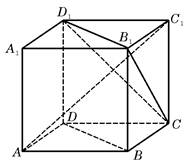
如图,已知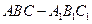 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是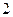 .
.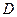 为侧棱
为侧棱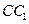 的中点,
的中点,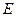 为底面一边
为底面一边 的中点.
的中点.
(1)求异面直线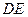 与
与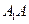 所成的角;
所成的角;
(2)求证: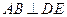 ;
;
(3)求直线 到平面
到平面 的距离.
的距离.
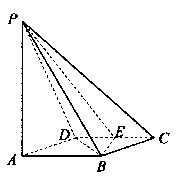
 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是 .
.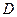 为侧棱
为侧棱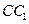 的中点,
的中点,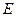 为底面一边
为底面一边 的中点.
的中点.(1)求异面直线
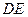 与
与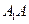 所成的角;
所成的角;(2)求证:
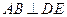 ;
;(3)求直线
 到平面
到平面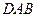 的距离.
的距离.
(1)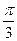 (2)证明见解析 (3)
(2)证明见解析 (3)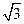
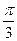 (2)证明见解析 (3)
(2)证明见解析 (3)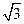
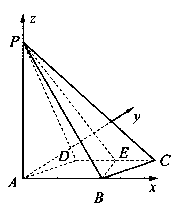
(1)取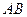 中点
中点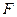 ,连结
,连结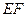 ,
,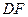 ,
,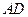 ,
,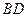 .则
.则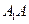
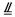
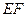 .
.
∴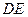 与
与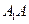 所成的角即为
所成的角即为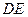 与
与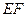 所成的角
所成的角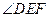 ,
,
∵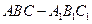 是正三棱柱,且各棱长均为
是正三棱柱,且各棱长均为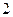 ,∴
,∴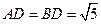 ,
,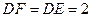 ,
,
∴△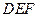 为正三角形,故
为正三角形,故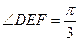 ,即异面直线
,即异面直线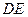 与
与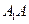 所成的角为
所成的角为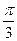 .
.
(2)由(1)知,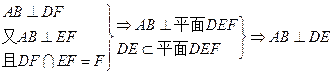 .
.
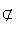 (3)
(3)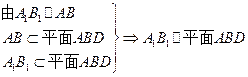 ,
,
∴点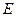 到平面
到平面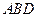 的距离,即为直线
的距离,即为直线 到平面
到平面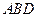 的距离,由(2)易证:平面
的距离,由(2)易证:平面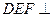 平面
平面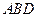 ,且交线为
,且交线为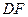 ,过
,过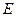 作
作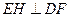 于点
于点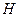 ,则
,则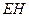 为点
为点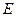 到平面
到平面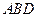 的距离,由(1)知,△
的距离,由(1)知,△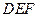 为正三角形且边长为
为正三角形且边长为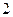 ,∴
,∴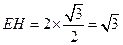 ,所以直线
,所以直线 到平面
到平面 的距离为
的距离为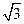 .
.
 中点
中点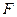 ,连结
,连结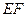 ,
,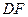 ,
,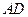 ,
,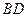 .则
.则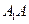
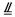
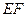 .
.
∴
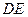 与
与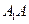 所成的角即为
所成的角即为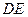 与
与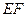 所成的角
所成的角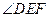 ,
,∵
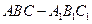 是正三棱柱,且各棱长均为
是正三棱柱,且各棱长均为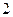 ,∴
,∴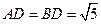 ,
,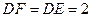 ,
,∴△
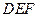 为正三角形,故
为正三角形,故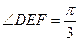 ,即异面直线
,即异面直线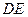 与
与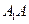 所成的角为
所成的角为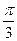 .
. (2)由(1)知,
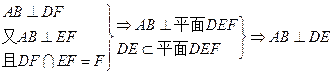 .
. (3)
(3)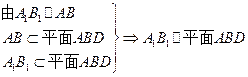 ,
,∴点
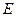 到平面
到平面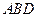 的距离,即为直线
的距离,即为直线 到平面
到平面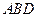 的距离,由(2)易证:平面
的距离,由(2)易证:平面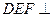 平面
平面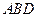 ,且交线为
,且交线为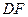 ,过
,过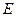 作
作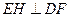 于点
于点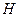 ,则
,则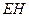 为点
为点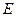 到平面
到平面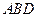 的距离,由(1)知,△
的距离,由(1)知,△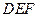 为正三角形且边长为
为正三角形且边长为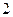 ,∴
,∴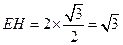 ,所以直线
,所以直线 到平面
到平面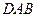 的距离为
的距离为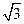 .
. 
练习册系列答案
相关题目
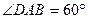 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面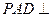 底面ABCD,且
底面ABCD,且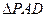 为等腰直角三角形,
为等腰直角三角形,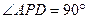 ,M为AP的中点。
,M为AP的中点。 (1)求证:
(1)求证: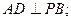
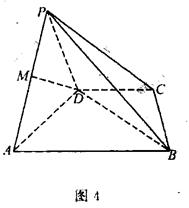
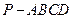 的底面
的底面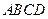 是边长为1的菱形,
是边长为1的菱形,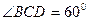 ,
, 底面ABCD,
底面ABCD, 。
。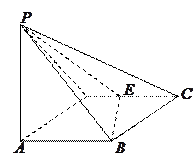
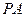 垂直于
垂直于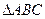 所在平面,
所在平面,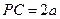 ,
,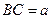 ,
,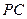 与平面
与平面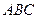 成
成 角,又
角,又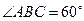 ,①求证:
,①求证: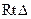 ;②求
;②求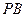 与平面
与平面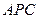 所成的角的正切值.
所成的角的正切值.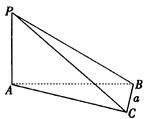
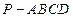 中,面
中,面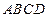 为矩形,
为矩形, 面
面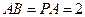
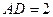 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;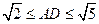 时,求二面角
时,求二面角 的取值范围。
的取值范围。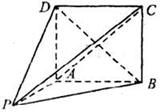

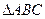
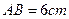
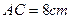
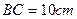
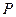
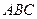
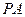 与平面
与平面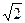 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=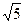 ,求AB、BC的长.
,求AB、BC的长.
 ,有下面四个命题:
,有下面四个命题: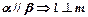 ; (2)
; (2)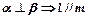 ;
; 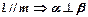 ; (4)
; (4)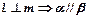 .
.