题目内容
【题目】函数y=Asin(ωx+)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值﹣3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( ![]() )>Asin(
)>Asin( ![]() )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
【答案】
(1)
解:∵当x=π时,y有最大值3,当x=6π时,y有最小值﹣3.
∴A= ![]() [3﹣(﹣3)]=3,
[3﹣(﹣3)]=3, ![]() =5π,
=5π,
∴T=10π= ![]() ,
,
∴ω= ![]() =
= ![]() ,
,
∵当x=π时,y有最大值3,
∴ ![]() π+=
π+= ![]() ,
,
∴= ![]() ,
,
∴y=3sin( ![]() x+
x+ ![]() ),
),
(2)
解:令 2kπ﹣ ![]() ≤
≤ ![]() x+
x+ ![]() ≤2kπ+
≤2kπ+ ![]() 得10kπ﹣4π≤x≤10kπ+π,k∈Z
得10kπ﹣4π≤x≤10kπ+π,k∈Z
∴函数的单调递增区间为:{x|10kπ﹣4π≤x≤10kπ+π k∈Z};
(3)
解:∵ω= ![]() ,=
,= ![]() ,
,
∴ω ![]() +=
+= ![]()
![]() +
+ ![]() ∈(0,
∈(0, ![]() ),
),
ω ![]() +=
+= ![]()
![]() +
+ ![]() ∈(0,
∈(0, ![]() ),
),
而y=sint在(0, ![]() )上是增函数
)上是增函数
∴ ![]()
![]() +
+ ![]() >
> ![]()
![]() +
+ ![]() ,
,
∴ ![]() >
> ![]()
∴ 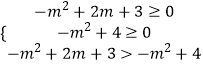 ,
,
∴ 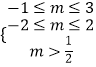 解得:
解得: ![]() .
.
∴m的取值范围是 ![]() .
.
【解析】(1)根据题意,函数的最值可以确定A,根据在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值﹣3,可以确定函数的周期,从而求出ω的值和φ的值,从而求得函数的解析式;(2)令 2kπ﹣ ![]() ≤
≤ ![]() x+
x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,解此不等式,即可求得函数的单调递增区间;(3)根据(1)所求得的ω和φ的值,分析
,解此不等式,即可求得函数的单调递增区间;(3)根据(1)所求得的ω和φ的值,分析 ![]() 和
和 ![]() 的范围,确定函数在该区间上的单调性,即可求得结果.
的范围,确定函数在该区间上的单调性,即可求得结果.
【考点精析】根据题目的已知条件,利用正弦函数的单调性的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.

【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
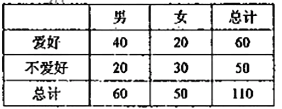
由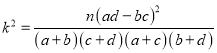 算得,
算得, ![]() .
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则参照附表,得到的正确结论应是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”