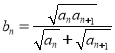题目内容
【题目】已知函数f（x）=|lgx|﹣（ 
）x有两个零点x1 ， x2 ， 则有（ ）
A.x1x2＜0
B.x1x2=1
C.x1x2＞1
D.0＜x1x2＜1
【答案】D
【解析】解：f（x）=|lgx|﹣（ 
）x有两个零点x1 ， x2
即y=|lgx|与y=2﹣x有两个交点
由题意x＞0，分别画y=2﹣x和y=|lgx|的图象
发现在（0，1）和（1，+∞）有两个交点
不妨设 x1在（0，1）里 x2在（1，+∞）里
那么 在（0，1）上有 2﹣x1=﹣lgx1 ， 即﹣2﹣x1=lgx1…①
在（1，+∞）有2﹣x2=lg x2…②
①②相加有2﹣x2﹣2﹣x1=lgx1x2
∵x2＞x1 ， ∴2﹣x2＜2﹣x1 即2﹣x2﹣2﹣x1＜0
∴lgx1x2＜0
∴0＜x1x2＜1
故选D．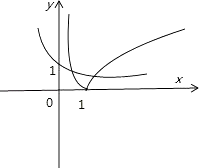
先将f（x）=|lgx|﹣（ ）x有两个零点转化为y=|lgx|与y=2﹣x有两个交点，然后在同一坐标系中画出两函数的图象得到零点在（0，1）和（1，+∞）内，即可得到﹣2﹣x1=lgx1和2﹣x2=lg x2 ， 然后两式相加即可求得x1x2的范围．
练习册系列答案
相关题目
