题目内容
【题目】已知f（x）是二次函数，且f（0）=0，f（x+1）=f（x）+x+1，
（1）求f（x）的表达式；
（2）若f（x）＞a在x∈[﹣1，1]恒成立，求实数a的取值范围．
【答案】
（1）解：设f（x）=ax2+bx+c∵f（0）=0∴c=0
∴f（x）=ax2+bxf（x）+x+1=ax2+（b+1）x+1f（x+1）
=a（x+1）2+b（x+1）=ax2+（2a+b）x+a+b∵f（x+1）
=f（x）+x+1∴ax2+（2a+b）x+a+b=ax2+（b+1）x+1
∴ 
∴ 
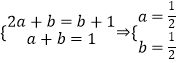（2）解：f（x）＞a在x∈[﹣1，1]恒成立
∴ 
x＞a在x∈[﹣1，1]恒成立
∴ 
在x∈[﹣1，1]恒成立．
∴ 
【解析】（1）根据函数类型设出函数的解析式，然后根据f（0）=0，f（x+1）=f（x）+x+1，建立两个等式关系，解之即可；（2）要使f（x）＞a在x∈[﹣1，1]恒成立，只需研究函数f（x）在闭区间[﹣1，1]上的最小值即可，利用配方法结合二次函数的性质即可求出f（x）的最小值．
练习册系列答案
相关题目
